D
分析:由于函数f(x)为分段函数,故要使其为单调增函数,需每段上为增函数且x<0时的最大值小于或等于x≥0时的最小值,同理得出其为单调减函数的条件,因此先求函数为增函数的充要条件,再比较选项中的集合与充要条件集合的包含关系即可判断其充要性.
解答:函数f(x)=
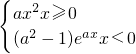
,为分段函数,
(1)当函数f(x)=
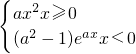
在(-∞,+∞)上是单调增函数时,
当x≥0时,y=ax
2为二次函数,图象是对称轴为y轴的抛物线,它为增函数时,有a>0;
当x<0时,f(x)=(a
2-1)e
ax是增函数,它的导函数为f′(x)=a(a
2-1)e
ax,
令f′(x)≥0得-1≤a≤0或a≥1,且(a
2-1)e
0≤0即-1≤a≤1,
∴综合得a=1;
(2)当函数f(x)=
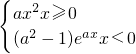
在(-∞,+∞)上是单调减函数时,
当x≥0时,y=ax
2为二次函数,图象是对称轴为y轴的抛物线,它为减函数时,有a<0;
当x<0时,f(x)=(a
2-1)e
ax是减函数,它的导函数为f′(x)=a(a
2-1)e
ax,
令f′(x)≤0得
0≤a≤1或a≤-1,
且(a
2-1)e
0≥0即a≤-1或a≥1,
∴综合得a≤-1.
综上所述,函数f(x)=
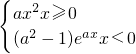
在(-∞,+∞)上是单调函数的充要条件是a≤-1或a=1,
∵选项D:“
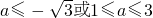
”?a≤-1或a=1,反之不成立.
∴选项D:“
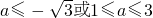
”是“f(x)在R上单调递增”的必要不充分条件.
故选D.
点评:本题考查了分段函数的单调性的判断方法,判断命题充要性的方法,导函数的应用等,属于基础题.

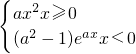 在(-∞,+∞)上是单调函数的必要不充分条件是
在(-∞,+∞)上是单调函数的必要不充分条件是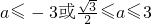
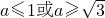

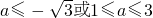
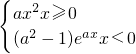 ,为分段函数,
,为分段函数,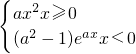 在(-∞,+∞)上是单调增函数时,
在(-∞,+∞)上是单调增函数时,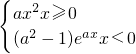 在(-∞,+∞)上是单调减函数时,
在(-∞,+∞)上是单调减函数时,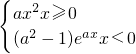 在(-∞,+∞)上是单调函数的充要条件是a≤-1或a=1,
在(-∞,+∞)上是单调函数的充要条件是a≤-1或a=1,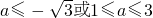 ”?a≤-1或a=1,反之不成立.
”?a≤-1或a=1,反之不成立.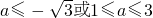 ”是“f(x)在R上单调递增”的必要不充分条件.
”是“f(x)在R上单调递增”的必要不充分条件.
