
 如图,在直角梯形ABCD中,AB⊥AD,AB∥DC,AB=2,AD=DC=1,图中圆弧所在圆的圆心为点C,半径为$\frac{1}{2}$,且点P在图中阴影部分(包括边界)运动.若$\overrightarrow{AP}$=x$\overrightarrow{AB}$+y$\overrightarrow{BC}$,其中x,y∈R,则4x-y的取值范围是( )
如图,在直角梯形ABCD中,AB⊥AD,AB∥DC,AB=2,AD=DC=1,图中圆弧所在圆的圆心为点C,半径为$\frac{1}{2}$,且点P在图中阴影部分(包括边界)运动.若$\overrightarrow{AP}$=x$\overrightarrow{AB}$+y$\overrightarrow{BC}$,其中x,y∈R,则4x-y的取值范围是( )| A. | $[2,\;\;3+\frac{{3\sqrt{2}}}{4}]$ | B. | $[2,\;\;3+\frac{{\sqrt{5}}}{2}]$ | ||
| C. | $[3-\;\;\frac{{\sqrt{2}}}{4},\;\;3+\frac{{\sqrt{5}}}{2}]$ | D. | $[3-\;\;\frac{{\sqrt{17}}}{2},\;\;3+\;\frac{{\sqrt{17}}}{2}]$ |
分析 建立直角坐标系,写出点的坐标与圆的方程;
设出点P的坐标,求出三个向量坐标,将P的坐标代入圆的方程求出4x-y的取值范围.
解答 解:以A为坐标原点,AB为x轴,DA为y轴建立平面直角坐标系则
A(0,0),D(0,1),C(1,1),B(2,0)
直线BD的方程为x+2y-2=0,C到BD的距离d=$\frac{\sqrt{5}}{5}$;
∴以点C为圆心,以$\frac{1}{2}$为半径的圆方程为(x-1)2+(y-1)2=$\frac{1}{4}$,
设P(m,n)则 $\overrightarrow{AP}$=(m,n),$\overrightarrow{AB}$=(2,0),$\overrightarrow{BC}$=(-1,1);
∴(m,n)=(2x-y,y)
∴m=2x-y,n=y,
∵P在圆内或圆上
∴(2x-y-1)2+(y-1)2≤$\frac{1}{4}$,
设4x-y=t,则y=4x-t,代入上式整理得
80x2-(48t+32)x+8t2+7≤0,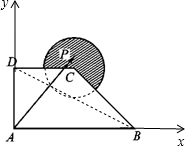
设f(x)=80x2-(48t+32)x+8t2+7,x∈[$\frac{1}{2}$,$\frac{3}{2}$],
则$\left\{\begin{array}{l}{f(\frac{1}{2})≤0}\\{f(\frac{3}{2})≤0}\end{array}\right.$,
解得2≤t≤3+$\frac{\sqrt{5}}{2}$,
∴4x-y的取值范围是[2,3+$\frac{\sqrt{5}}{2}$].
故选:B.
点评 本题考查了直线与圆的应用问题,也考查了数形结合应用问题,是综合题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 第一批次 | 第二批次 | 第三批次 | |
| 女教职工 | 196 | x | y |
| 男教职工 | 204 | 156 | z |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 共线 | B. | 不共线 | C. | 不共面 | D. | 以上都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2015-2016学年江西省南昌市高二理下学期期末考试数学试卷(解析版) 题型:解答题
一个袋子装有大小形状完全相同的9个球,其中5个红球编号分别为1,2,3,4,5;4个白球编号分别为1,2,3,4,从袋中任意取出3个球.
(I)求取出的3个球编号都不相同的概率;
(II)记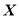 为取出的3个球中编号的最小值,求
为取出的3个球中编号的最小值,求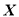 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com