
分析 先求出基本事件(a,b)的个数n=4×4=16,再利用列举法求出函数y=ax+b的图象经过第三象限的情况,由此能求出函数y=ax+b的图象经过第三象限的概率.
解答 解:从集合{$\frac{1}{2}$,$\frac{1}{3}$,2,3}中任取一个数记做a,从集合{-2,-1,1,2}中任取一个数记做b,
基本事件(a,b)的个数n=4×4=16,
∵函数y=ax+b的图象经过第三象限有:
①当a=3、b=-1时,②当a=3、b=-2时,③当a=2、b=-1时,
④当a=2、b=-2时,⑤当a=$\frac{1}{3}$,b=-2 时,⑥当a=$\frac{1}{2}$,b=-2 时,共6种情况,
∴函数y=ax+b的图象经过第三象限的概率是p=$\frac{6}{16}=\frac{3}{8}$.
故答案为:$\frac{3}{8}$.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.


 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案科目:高中数学 来源: 题型:选择题
| X | 1 | 2 | 3 |
| P | P1 | P2 | P3 |
| A. | P1=P2 | B. | P2=P3 | C. | P1=P3 | D. | P1=P2=P3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若α⊥β,β⊥γ,则α∥γ | |
| B. | 若m?α,n?β,m∥n,则α∥β | |
| C. | 若m,n是异面直线,m?α,m∥β,n?β,n∥α,则α∥β | |
| D. | 平面α内有不共线的三点到平面β的距离相等,则α∥β |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2015-2016学年河北省保定市高一上学期期中考试数学试卷(解析版) 题型:选择题
如图①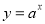 ,②
,② ,③
,③ ,④
,④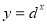 ,根据图象可得a、b、c、d与1的大小关系为( )
,根据图象可得a、b、c、d与1的大小关系为( )

A.a<b<1<c<d B.b<a<1<d<c
C.1<a<b<c<d D.a<b<1<d<c
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com