
分析 (Ⅰ)根据题意,由向量平行的坐标公式可得-2x=4,解可得x的值,即可得答案;
(Ⅱ)若$\vec a⊥\vec b$,则有$\overrightarrow{a}$•$\overrightarrow{b}$=0,结合向量数量积的坐标可得4×x+(-2)×1=0,即4x-2=0,解可得x的值,即可得答案;
(Ⅲ)根据题意,由x的值可得$\overrightarrow{b}$的坐标,由向量的坐标计算公式可得|$\overrightarrow{a}$|、|2$\overrightarrow{b}$+$\overrightarrow{a}$|和$\overrightarrow{a}$•(2$\overrightarrow{b}$+$\overrightarrow{a}$)的值,结合$cosθ=\frac{\vec a•(2\vec b+\overrightarrow a)}{{|{\vec a}|•|{2\vec b+\overrightarrow a}|}}$,计算可得答案.
解答 解:( I)根据题意,向量$\overrightarrow a=(4,-2)$,$\overrightarrow b=(x,1)$,
若$\vec a与\vec b共线$,则有-2x=4,解可得x=-2.
( II)若$\vec a⊥\vec b$,则有$\overrightarrow{a}$•$\overrightarrow{b}$=0,
又由向量$\overrightarrow a=(4,-2)$,$\overrightarrow b=(x,1)$,
则有4×x+(-2)×1=0,即4x-2=0,
解可得$x=\frac{1}{2}$,
( III)根据题意,若$x=2,\vec b=(2,1)$,
则有$2\vec b+\overrightarrow a$=(8,0),$|{\vec a}|=\sqrt{{4^2}+{{(-2)}^2}}=2\sqrt{5},|{2\vec b+\overrightarrow a}|=\sqrt{{8^2}+0}=8$
$又∵\vec a•(2\vec b+\overrightarrow a)=32$,
∴$cosθ=\frac{\vec a•(2\vec b+\overrightarrow a)}{{|{\vec a}|•|{2\vec b+\overrightarrow a}|}}=\frac{32}{{16\sqrt{5}}}=\frac{{2\sqrt{5}}}{5}$.
点评 本题考查向量的数量积的运算,涉及平面向量的坐标计算,


 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{π}{3}$个单位长度 | B. | 向左平移$\frac{π}{6}$个单位长度 | ||
| C. | 向右平移$\frac{π}{3}$个单位长度 | D. | 向右平移$\frac{π}{6}$个单位长度 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 使用年数x | 2 | 3 | 4 | 5 | 6 | 7 |
| 售价y | 20 | 12 | 8 | 6.4 | 4.4 | 3 |
| z=lny | 3.00 | 2.48 | 2.08 | 1.86 | 1.48 | 1.10 |
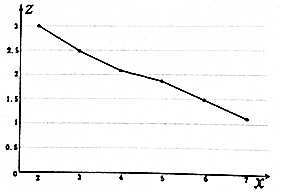
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y与x具有正线性相关关系 | |
| B. | 回归直线过样本的中心点$(\overline x,\overline y)$ | |
| C. | 若该中学某高中女生身高增加1cm,则其体重约增加0.85kg | |
| D. | 若该中学某高中女生身高为160cm,则可断定其体重必为50.29kg |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com