
分析 (1)由题意,ax2-bx+2>0(a>0)的解集为{x|x>2或x<1},根据不等式与方程的关系有:x1=2,x2=1求解a,b.
(2)b=2a+1,那么:f(x)=ax2-(2a+1)x+2=(ax-2)(x-1)≤0.对a与1的大小比较近讨论,得解.
解答 解:(1)由题意,ax2-bx+2>0(a>0)的解集为{x|x>2或x<1},根据不等式与方程的关系有:x1=2,x2=1,利用韦达定理:$\frac{b}{a}={x}_{1}+{x}_{2}=3$,$\frac{c}{a}={x}_{1}•{x}_{2}=2$,解得:a=1,b=3.
故当不等式f(x)>0的解集为{x|x>2或x<1},a、b的值分别为1,3;
(2)当b=2a+1,那么:f(x)=ax2-(2a+1)x+2=(ax-1)(x-2)
f(x)≤0,即(ax-1)(x-2)≤0,
解得:x1=$\frac{1}{a}$,x2=2.
当0<a<$\frac{1}{2}$时,x1>x2,不等式的解集为[$2,\frac{1}{a}$]
当a=$\frac{1}{2}$时,x1=x2,不等式的解集为{x|x=2};
当a>$\frac{1}{2}$时,x1<x2,不等式的解集为[$\frac{1}{a}$,2];
综上所述:当0<a<$\frac{1}{2}$时,x1>x2,不等式的解集为[$2,\frac{1}{a}$]
当a=$\frac{1}{2}$时,x1=x2,不等式的解集为{x|x=2};
当a>$\frac{1}{2}$时,x1<x2,不等式的解集为[$\frac{1}{a}$,2].
点评 本题主要考查了一元二次不等式的应用,以及根与系数的关系,同时考查了分析求解的能力和计算能力,属于中档题.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:高中数学 来源: 题型:解答题
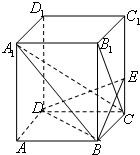 如图,已知正四棱柱ABCD-A1B1C1D1中,2AB=BB1,过点B作B1C的垂线交侧棱CC1于点E.
如图,已知正四棱柱ABCD-A1B1C1D1中,2AB=BB1,过点B作B1C的垂线交侧棱CC1于点E.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x=$\frac{kπ}{2}$-$\frac{π}{6}$ (k∈Z) | B. | x=$\frac{kπ}{2}$+$\frac{π}{6}$ (k∈Z) | C. | x=$\frac{kπ}{2}$-$\frac{π}{12}$ (k∈Z) | D. | x=$\frac{kπ}{2}$+$\frac{π}{12}$ (k∈Z) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,2) | B. | (1,2) | C. | (2,+∞) | D. | (1,2)∪(2,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com