
分析 (Ⅰ)利用f(-1)=kf(1),由 f(0.5)=k f(2.5),得到f(2.5)=$\frac{1}{k}$f(0.5)=$\frac{1}{k}$(0.5-2)•0.5.
(Ⅱ)条件可得f(x)=$\frac{1}{k}$f(x-2),当-2≤x<0时,-3≤x<-2时,分别求出f(x)的解析式,从而得到f(x)在[-3,3]上的表达式,通过表达式研究单调性.
(Ⅲ)由(Ⅱ)中函数f(x)在[-3,3]上的单调性可知,在x=-3或x=1处取最小值,在x=-1或x=3处取最大值.
解答 解:(Ⅰ)∵在区间[0,2]上有f(x)=x(x-2),∴f(1)=-1.
∵f(x)=kf(x+2),∴f(x+2)=$\frac{f(x)}{k}$,即f(x)=$\frac{1}{k}$f(x-2).
∴f(2.5)=f(2+0.5)=$\frac{1}{k}$•f(0.5)=$\frac{1}{k}$•(-$\frac{3}{4}$)=-$\frac{3}{4k}$.
(Ⅱ)当-2≤x<0时,0≤x+2<2,f(x)=kf(x+2)=kx(x+2);
当-3≤x<-2时,1≤x+4<2,f(x)=kf(x+2)=k2 •f(x+4)=(x+4)(x+2).
当2≤x≤3 时,0≤x-2≤1,f(x-2)=kf(x)=(x-2)(x-4),故f(x)=$\frac{1}{k}$(x-2)(x-4).
综上可得,f(x)=$\left\{\begin{array}{l}{{k}^{2}(x+2)(x+4),-3≤x<-2}\\{kx(x+2),-2≤x<0}\\{x(x-2),0≤x<2}\\{\frac{1}{k}(x-2)(x-4),2≤x≤3}\end{array}\right.$.
(Ⅲ)∵k<0,∴f(x)在[-3,-1]与[1,3]上为增函数,在[-1,1]上为减函数,
故f(x)在x=-3或x=1处取最小值为 f(-3)=-k2,或f(1)=-1,
而在x=-1或x=3处取最大值为 f(-1)=-k,或f(3)=-$\frac{1}{k}$,
故有:
①k<-1时,f(x)在x=-3处取最小值f(-3)=-k2,在x=-1处取最大值f(-1)=-k;
②k=-1时,f(x)在x=-3与x=1处取最小值f(-3)=f(1)=-1,在x=-1与x=3处取最大值f(-1)=f(3)=1;
③-1<k<0时,f(x)在x=1处取最小值f(1)=-1,在x=3处取最大值f(3)=-$\frac{1}{k}$.
点评 这是一道求函数解析式的问题,本题较为抽象,在区间转化时一定要细心,防止出错,属于难题.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-1,\frac{1}{3}$ | B. | $1,\frac{2}{3}$ | C. | $1,\frac{1}{3}$ | D. | $1,\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,+∞) | B. | (-∞,1] | C. | [-3,+∞) | D. | (-∞,-3] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
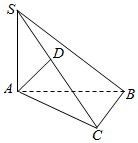 已知△ABC中∠ACB=90°,SA⊥面ABC,AD⊥SC,
已知△ABC中∠ACB=90°,SA⊥面ABC,AD⊥SC,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1对 | B. | 2对 | C. | 3对 | D. | 4对 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com