
分析 根据二项式定理,512015+1=(52-1)2015+1展开后即可判断.
解答 解:512015+1=(52-1)2015+1=C20150•522015•(-1)0+C20151•522014•(-1)1+C20152•522013•(-1)2+…+C20152014•521•(-1)2014+C20152015•520•(-1)2015+1
=C20150•522015•(-1)0+C20151•522014•(-1)1+C20152•522013•(-1)2+…+C20152014•521•(-1)2014,
因为每一项都有52,且52能被13整除,
故512015+1被13整除,
则512015除以13,所得余数为12,
故答案为:12.
点评 本题考查了数的整除问题,利用二项式定理是关键,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
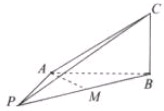 如图,PA⊥平面ABC,AB⊥BC,AB=PA=2BC=2,M为PB的中点.
如图,PA⊥平面ABC,AB⊥BC,AB=PA=2BC=2,M为PB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | -1 | C. | 1 | D. | e |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com