
分析 由抛物线方程求出焦点坐标,设出E的坐标(-$\frac{1}{2}$,m),利用EF和QP垂直求得m的值,则EF、QP的方程可求,求出EF的长度,求出P的坐标,由三角形的面积公式求得△PEF的面积.
解答 解:如图, 由抛物线方程为y2=2x,得F($\frac{1}{2}$,0),设E(-$\frac{1}{2}$,m)(m>0),
由抛物线方程为y2=2x,得F($\frac{1}{2}$,0),设E(-$\frac{1}{2}$,m)(m>0),
则EF中点为G(0,$\frac{m}{2}$),kEF=-m,
又Q(-$\frac{1}{2}$,$\frac{3}{4}$),
∴kQG=$\frac{\frac{3}{4}-\frac{m}{2}}{-\frac{1}{2}-0}$=$\frac{2m-3}{2}$,
由kEF•kQG=-1,即-m•$\frac{2m-3}{2}$=-1,解得:m=2.
∴E(-$\frac{1}{2}$,2),
则|EF|=$\sqrt{(-\frac{1}{2}-\frac{1}{2})^{2}+(2-0)^{2}}$=$\sqrt{5}$,直线EF的方程为$\frac{y-0}{2-0}$=$\frac{x-\frac{1}{2}}{-\frac{1}{2}-\frac{1}{2}}$,化为一般式得:2x+y-1=0.
QG所在直线方程为y-1=-$\frac{1}{2}$x,即x-2y+2=0.
联立$\left\{\begin{array}{l}{x-2y+2=0}\\{{y}^{2}=2x}\end{array}\right.$,得$\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$,即P(2,2),
∴P到直线EF的距离为d=$\frac{丨2×2+2-1丨}{\sqrt{{2}^{2}+{1}^{2}}}$=$\sqrt{5}$.
则△PEF的面积为S=$\frac{1}{2}$×d×|EF|=$\frac{1}{2}$×$\sqrt{5}$×$\sqrt{5}$=$\frac{5}{2}$.
故答案为:$\frac{5}{2}$.
点评 本题考查了抛物线的简单性质,考查了抛物线的与平面解析式的综合应用.考查了考生的基础知识的综合运用和知识迁移的能力,属于中档题.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:选择题
| A. | ($\frac{8}{3}$,$\frac{28}{5}$) | B. | ($\frac{8}{3}$,$\frac{28}{5}$] | C. | ($\frac{8}{3}$,$\frac{18}{5}$) | D. | ($\frac{8}{3}$,$\frac{18}{5}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
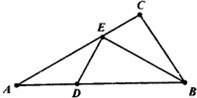 如图,在Rt△ABC中,∠C=90°,BE平分∠ABC,交AC于点E,过点E作ED⊥BE交AB于点D.
如图,在Rt△ABC中,∠C=90°,BE平分∠ABC,交AC于点E,过点E作ED⊥BE交AB于点D.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
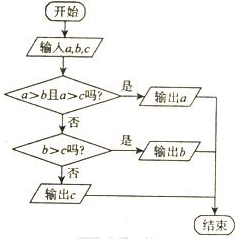 如图所示的流程图是将一系列指令和问题用框图的形式排列而成.箭头说明下一步是到哪一个框图,阅读这个流程图,回答下列问题:
如图所示的流程图是将一系列指令和问题用框图的形式排列而成.箭头说明下一步是到哪一个框图,阅读这个流程图,回答下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 45° | B. | 90° | C. | 60° | D. | 30° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com