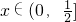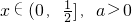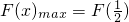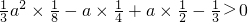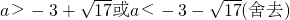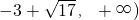解:∵f′(x)=a
2x
2-2ax
(I)当a=1时,f′(1)=-1,f(1)=0
所以f(x)在点(1,f(1))的切线方程为y=-x+1
(II)令f′(x)=0得
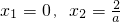
(1)当
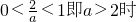
,
x∈(-1,0)时,f′(x)>0,f(x)递增

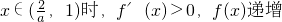
所以当x=0时,有极大值

;当

有极小值

(2)当
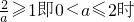
,f(x)在(-1,0)上递增,在(0,1)递减
所以f(x)极大值为f(0)=

,无极小值
(III)设F(x)=f(x)-g(x)=
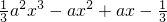
,
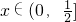
F′(x)=a
2x
2-2ax+a=a
2x
2+a(1-2x)
∵
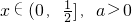
∴F′(x)=a
2x
2+a(1-2x)>0
∴

则
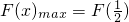
依题意,只需F(x)
max>0
即
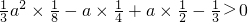
解得
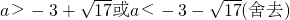
所以实数a的取值范围是(
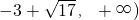
分析:(I)求出函数在x=1处的导数即切线的斜率,利用直线方程的点斜式求出切线的方程.
(II)求出导函数,令导函数为求出两个根,两个的大小引起讨论;判断导函数在根左右两边的符号,判断出函数的单调性,利用极值的定义求出函数的极值.
(III)构造新函数,求出新函数的导数,通过导函数的符号判断函数的单调性,求出函数的最大值,将问题转化为最大值大于0,求出a的范围.
点评:本题考查导数的几何意义|在切点处的导数值是切线的斜率、考查利用导数求函数的单调性、求函数的极值、求函数的最值、考查不等式有解问题等价转化为函数的最值问题.

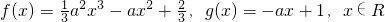 .
.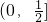 上至少存在一个实数x0,使f(x0)>g(x0)成立,求正实数a的取值范围.
上至少存在一个实数x0,使f(x0)>g(x0)成立,求正实数a的取值范围.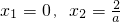
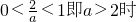 ,
,
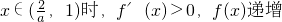
 ;当
;当 有极小值
有极小值
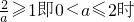 ,f(x)在(-1,0)上递增,在(0,1)递减
,f(x)在(-1,0)上递增,在(0,1)递减 ,无极小值
,无极小值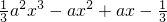 ,
,