
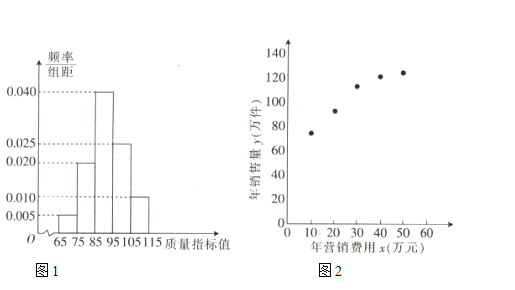
【题目】某企业生产一种产品,从流水线上随机抽取![]() 件产品,统计其质量指标值并绘制频率分布直方图(如图1):规定产品的质量指标值在
件产品,统计其质量指标值并绘制频率分布直方图(如图1):规定产品的质量指标值在![]() 的为劣质品,在
的为劣质品,在![]() 的为优等品,在
的为优等品,在![]() 的为特优品,销售时劣质品每件亏损
的为特优品,销售时劣质品每件亏损![]() 元,优等品每件盈利
元,优等品每件盈利![]() 元,特优品每件盈利
元,特优品每件盈利![]() 元,以这
元,以这![]() 件产品的质量指标值位于各区间的频率代替产品的质量指标值位于该区间的概率.
件产品的质量指标值位于各区间的频率代替产品的质量指标值位于该区间的概率.
(1)求每件产品的平均销售利润;
(2)该企业主管部门为了解企业年营销费用![]() (单位:万元)对年销售量
(单位:万元)对年销售量![]() (单位:万件)的影响,对该企业近
(单位:万件)的影响,对该企业近![]() 年的年营销费用
年的年营销费用![]() 和年销售量
和年销售量![]() ,
,![]() 数据做了初步处理,得到的散点图(如图2)及一些统计量的值.
数据做了初步处理,得到的散点图(如图2)及一些统计量的值.
|
|
|
|
|
|
|
|
表中![]() ,
,![]() ,
,![]() ,
,![]() .
.
根据散点图判断,![]() 可以作为年销售量
可以作为年销售量![]() (万件)关于年营销费用
(万件)关于年营销费用![]() (万元)的回归方程.
(万元)的回归方程.
①求![]() 关于
关于![]() 的回归方程;
的回归方程;
②用所求的回归方程估计该企业每年应投入多少营销费,才能使得该企业的年收益的预报值达到最大?(收益![]() 销售利润
销售利润![]() 营销费用,取
营销费用,取![]() )
)
附:对于一组数据![]() ,
,![]() ,
,![]() ,
,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为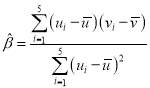 ,
,![]() .
.
【答案】(1)![]() 元.(2)①
元.(2)①![]() ②
②![]() 万元
万元
【解析】
(1)每件产品的销售利润为![]() ,由已知可得
,由已知可得![]() 的取值,由频率分布直方图可得劣质品、优等品、特优品的概率,从而可得
的取值,由频率分布直方图可得劣质品、优等品、特优品的概率,从而可得![]() 的概率分布列,依期望公式计算出期望即为平均销售利润;
的概率分布列,依期望公式计算出期望即为平均销售利润;
(2)①对![]() 取自然对数,得
取自然对数,得![]() ,
,
令![]() ,
,![]() ,
,![]() ,则
,则![]() ,这就是线性回归方程,由所给公式数据计算出系数,得线性回归方程,从而可求得
,这就是线性回归方程,由所给公式数据计算出系数,得线性回归方程,从而可求得![]() ;
;
②求出收益![]() ,可设
,可设![]() 换元后用导数求出最大值.
换元后用导数求出最大值.
解:(1)设每件产品的销售利润为![]() ,则
,则![]() 的可能取值为
的可能取值为![]() ,
,![]() ,
,![]() .由频率分布直方图可得产品为劣质品、优等品、特优品的概率分别为
.由频率分布直方图可得产品为劣质品、优等品、特优品的概率分别为![]() 、
、![]() 、
、![]() .
.
所以![]() ;
;![]() ;
;![]() .所以
.所以![]() 的分布列为
的分布列为
|
|
|
|
|
|
|
|
所以![]() (元).
(元).
即每件产品的平均销售利润为![]() 元.
元.
(2)①由![]() ,得
,得![]() ,
,
令![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,
由表中数据可得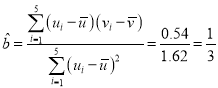 ,
,
则![]() ,
,
所以![]() ,即
,即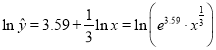 ,
,
因为取![]() ,所以
,所以![]() ,故所求的回归方程为
,故所求的回归方程为![]() .
.
②设年收益为![]() 万元,则
万元,则![]()
令![]() ,则
,则![]() ,
,![]() ,当
,当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,所以当
,所以当![]() ,即
,即![]() 时,
时,![]() 有最大值
有最大值![]() .
.
即该企业每年应该投入![]() 万元营销费,能使得该企业的年收益的预报值达到最大,最大收益为
万元营销费,能使得该企业的年收益的预报值达到最大,最大收益为![]() 万元.
万元.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源: 题型:
【题目】近几年,我国在电动汽车领域有了长足的发展,电动汽车的核心技术是动力总成,而动力总成的核心技术是电机和控制器,我国永磁电机的技术已处于国际领先水平.某公司计划今年年初用196万元引进一条永磁电机生产线,第一年需要安装、人工等费用24万元,从第二年起,包括人工、维修等费用每年所需费用比上一年增加8万元,该生产线每年年产值保持在100万元.
(1)引进该生产线几年后总盈利最大,最大是多少万元?
(2)引进该生产线几年后平均盈利最多,最多是多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,
中,![]() 的参数方程为
的参数方程为 (t为参数).以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为
(t为参数).以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]() .
.
(1)求![]() 的普通方程和曲线C的直角坐标方程;
的普通方程和曲线C的直角坐标方程;
(2)求曲线C上的点到![]() 距离的最大值及该点坐标.
距离的最大值及该点坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题![]() :函数
:函数![]() 的定义域为
的定义域为![]() ;命题
;命题![]() :不等式
:不等式![]() 对一切正实数
对一切正实数![]() 均成立.
均成立.
(1)如果![]() 是真命题,求实数
是真命题,求实数![]() 的取值范围;
的取值范围;
(2)如果命题“![]() ”为真命题,且“
”为真命题,且“![]() ”为假命题,求实数
”为假命题,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第十三届全国人大常委会第十一次会议审议的《固体废物污染环境防治法(修订草案)》中,提出推行生活垃圾分类制度,这是生活垃圾分类首次被纳入国家立法中.为了解某城市居民的垃圾分类意识与政府相关法规宣传普及的关系,对某试点社区抽取![]() 户居民进行调查,得到如下的
户居民进行调查,得到如下的![]() 列联表.
列联表.
分类意识强 | 分类意识弱 | 合计 | |
试点后 |
| ||
试点前 |
| ||
合计 |
|
已知在抽取的![]() 户居民中随机抽取
户居民中随机抽取![]() 户,抽到分类意识强的概率为
户,抽到分类意识强的概率为![]() .
.
(1)请将上面的![]() 列联表补充完整,并判断是否有
列联表补充完整,并判断是否有![]() 的把握认为居民分类意识的强弱与政府宣传普及工作有关?说明你的理由;
的把握认为居民分类意识的强弱与政府宣传普及工作有关?说明你的理由;
(2)已知在试点前分类意识强的![]() 户居民中,有
户居民中,有![]() 户自觉垃圾分类在
户自觉垃圾分类在![]() 年以上,现在从试点前分类意识强的
年以上,现在从试点前分类意识强的![]() 户居民中,随机选出
户居民中,随机选出![]() 户进行自觉垃圾分类年限的调查,记选出自觉垃圾分类年限在
户进行自觉垃圾分类年限的调查,记选出自觉垃圾分类年限在![]() 年以上的户数为
年以上的户数为![]() ,求
,求![]() 分布列及数学期望.
分布列及数学期望.
参考公式: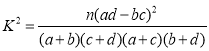 ,其中
,其中![]() .
.
下面的临界值表仅供参考
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
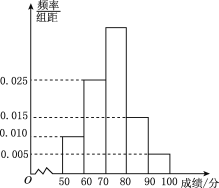
【题目】从2013年开始,国家教育部要求高中阶段每学年都要组织学生进行学生体质健康测试,方案要求以学校为单位组织实施,某校对高一(1)班学生根据《国家学生体质健康标准》的测试项目按百分制进行了预备测试,并对50分以上的成绩进行统计,其频率分布直方图如图.所示,已知[90,100]分数段的人数为2.
(1)求[70,80)分数段的人数;
(2)现根据预备测试成绩从成绩在80分以上(含80分)的学生中任意选出2人代表班级参加学校举行的一项体育比赛,求这2人的成绩一个在[80,90)分数段、一个在[90,100]分数段的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某汽车站每天均有3辆开往省城的分为上、中、下等级的客车,某天袁先生准备在该汽车站乘车前往省城办事,但他不知道客车的车况,也不知道发车顺序.为了尽可能乘上上等车,他采取如下策略:先放过一辆,如果第二辆比第一辆好则上第二辆,否则上第三辆.则他乘上上等车的概率为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,矩形![]() ,
,![]() 为
为![]() 的中点,将
的中点,将![]() 沿直线
沿直线![]() 翻折成
翻折成![]() ,连接
,连接![]() ,
,![]() 为
为![]() 的中点,则在翻折过程中,下列说法中所有正确的是( )
的中点,则在翻折过程中,下列说法中所有正确的是( )
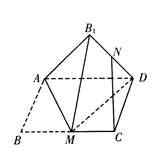
A.存在某个位置,使得![]() B.翻折过程中,
B.翻折过程中,![]() 的长是定值
的长是定值
C.若![]() ,则
,则![]() ;D.若
;D.若![]() ,当三棱锥
,当三棱锥![]() 的体积最大时,三棱锥
的体积最大时,三棱锥![]() 的外接球的表面积是
的外接球的表面积是![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com