
【题目】已知:以点![]() (
(![]() )为圆心的圆与
)为圆心的圆与![]() 轴交
轴交
于点O, A,与y轴交于点O, B,其中O为原点.
(1)求证:△OAB的面积为定值;
(2)设直线![]() 与圆C交于点M, N,若OM = ON,求圆C的方程.
与圆C交于点M, N,若OM = ON,求圆C的方程.
【答案】(1)根据条件写成圆的方程,求出点A,B的坐标,进而写出△OAB的面积即可得证;
(2)![]()
【解析】试题分析:(1)设出圆C的方程,求得A、B的坐标,再根据S△AOB=![]() OAOB,计算可得结论.
OAOB,计算可得结论.
(2)设MN的中点为H,则CH⊥MN,根据C、H、O三点共线,KMN=﹣2,由直线OC的斜率![]() ,求得t的值,可得所求的圆C的方程.
,求得t的值,可得所求的圆C的方程.
试题解析:
(1)![]() ,
,![]() .
.
设圆![]() 的方程是
的方程是 ![]()
令![]() ,得
,得![]() ;令
;令![]() ,得
,得![]()
![]() ,即:
,即:![]() 的面积为定值.
的面积为定值.
(2)![]()
![]() 垂直平分线段
垂直平分线段![]() .
.
![]() ,
,![]() 直线
直线![]() 的方程是
的方程是![]() .
.
![]() ,解得:
,解得:![]()
当![]() 时,圆心
时,圆心![]() 的坐标为
的坐标为![]() ,
,![]() ,此时
,此时![]() 到直线
到直线![]() 的距离
的距离![]() ,圆
,圆![]() 与直线
与直线![]() 相交于两点.
相交于两点.
当![]() 时,圆心
时,圆心![]() 的坐标为
的坐标为![]() ,
,![]() ,此时
,此时![]() 到直线
到直线![]() 的距离
的距离![]() 圆
圆![]() 与直线
与直线![]() 不相交,
不相交,![]() 不符合题意舍去.
不符合题意舍去.
![]() 圆
圆![]() 的方程为
的方程为![]() .
.


科目:高中数学 来源: 题型:
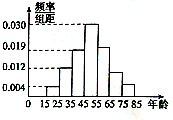
【题目】某购物中心为了了解顾客使用新推出的某购物卡的顾客的年龄分布情况,随机调查了![]() 位到购物中心购物的顾客年龄,并整理后画出频率分布直方图如图所示,年龄落在区间
位到购物中心购物的顾客年龄,并整理后画出频率分布直方图如图所示,年龄落在区间![]() 内的频率之比为
内的频率之比为![]() .
.
(1) 求顾客年龄值落在区间![]() 内的频率;
内的频率;
(2) 拟利用分层抽样从年龄在![]() 的顾客中选取
的顾客中选取![]() 人召开一个座谈会,现从这
人召开一个座谈会,现从这![]() 人中选出
人中选出![]() 人,求这两人在不同年龄组的概率.
人,求这两人在不同年龄组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随机抽取某中学甲、乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图7.

(1)根据茎叶图判断哪个班的平均身高较高;
(2)计算甲班的样本方差;
(3)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学,求身高为176cm的同学被抽中的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位每天的用电量![]() (度)与当天最高气温
(度)与当天最高气温![]() (℃)之间具有线性相关关系,下表是该单位随机统计4天的用电量与当天最高气温的数据.
(℃)之间具有线性相关关系,下表是该单位随机统计4天的用电量与当天最高气温的数据.
最高气温(℃) | 26 | 29 | 31 | 34 |
用电量 (度) | 22 | 26 | 34 | 38 |
(Ⅰ)根据表中数据,求出回归直线的方程![]() (其中
(其中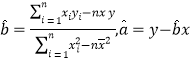 );
);
(Ⅱ)试预测某天最高气温为33℃时,该单位当天的用电量(精确到1度).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com