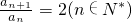Question

已知数列{a_n}的前n项和S_n=2a_n+1．
（ I）求证：数列{a_n}是等比数列；（ II）求出数列{a_n}的通项公式．

Answer 1

解：（ I）证明：依题意可得S_n+1=2a_n+1+1…①，S_n=2a_n+1…②
①-②，得a_n+1=2a_n+1-2a_n
化简得
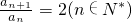
∴数列{a_n}是公比为2的等比数列．
（II）由（I）得，数列{a_n}是公比为2的等比数列，
把n=1代入S_n=2a_n+1，得S₁=a₁=2a₁+1，解得a₁=-1，
∴a_n=（-1）×2^n-1=-2^n-1．
分析：（I）把n=n+1代入S_n=2a_n+1得到一个式子，再把两个式子相减，再由S_n+1-S_n=a_n+1得到数列的递推公式，化简后根据等比数列的定义进行证明；
（II）把n=1代入S_n=2a_n+1，求出a₁的值，再由（I）的结论和等比数列的通项公式，求出a_n．
点评：本题考查了等比数列的定义和通项公式，以及S_n与a_n之间的关系的应用，证明数列是等比数列常用它的定义进行证明．