
【题目】如图,四棱锥P﹣ABCD的底面ABCD是平行四边形,PB⊥面ABCD,BA=BD= ![]() ,AD=2,E,F分别是棱AD,PC的中点.
,AD=2,E,F分别是棱AD,PC的中点. 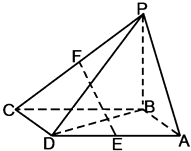
(1)证明:EF∥平面PAB;
(2)若二面角P﹣AD﹣B为60°,求直线EF与平面PBC所成角的正弦值.
【答案】
(1)证明:取PB的中点M,连接MF,AM.
又∵F为PC的中点,∴FM∥BC,FM= ![]() BC,(中位线定理),
BC,(中位线定理),
∵E为AD的中点,ABCD是平行四边形,
∴AE∥BC,AE= ![]() BC,
BC,
∴FM∥AE,FM=AE,
∴四边形AEFM为平行四边形
∴EF∥AM,
∵MA平面PAB,EF平面PAB,
∴EF∥平面PAB.

(2)解:∵BA=BD,PA=PD 且 E为AD的中点,
∴BE⊥AD,PE⊥AD,
∴∠PEB为二面角P﹣AD﹣B的平面角,∴∠PEB=60°,
∵在Rt△ABD,BA=BD= ![]() ,AD=2,
,AD=2,
∴BE=1,
∵∠PEB=60°,∴Rt△PBE中,PB= ![]() ,
,
∵BE⊥AD,AD∥BC,∴BE⊥BC,
∵PB⊥面ABCD,∴PB⊥BE,
由BC∩PB=B,∴BE⊥平面PBC,
∴∠EFB为直线EF与平面PBC所成角,
∵在Rt△ABM中,AM= ![]() ∴
∴ ![]() ,
,
∴在Rt△EBF中,sin∠EFB= ![]() =
= ![]() =
= ![]() ,
,
∴直线EF与平面PBC所成角的正弦值为 ![]()
【解析】(1)利用线面平行的判定定理或面面平行的性质定理证明.(2)根据二面角平面角的定义先找出平面角,结合直线和平面所成角的定义作出线面角,根据三角形的边角关系进行求解即可.
【考点精析】根据题目的已知条件,利用直线与平面平行的判定的相关知识可以得到问题的答案,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】过曲线y=x2(x≥0)上某一点A作一切线l,使之与曲线以及x轴所围成的图形的面积为 ![]() ,试求:
,试求:
(1)切点A的坐标;
(2)过切点A的切线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】海中一小岛![]() 的周围
的周围![]()
![]() 内有暗礁,海轮由西向东航行至
内有暗礁,海轮由西向东航行至![]() 处测得小岛
处测得小岛![]() 位于北偏东
位于北偏东![]() ,航行8
,航行8![]() 后,于
后,于![]() 处测得小岛
处测得小岛![]() 在北偏东
在北偏东![]() (如图所示).
(如图所示).

(1)如果这艘海轮不改变航向,有没有触礁的危险?请说明理由.
(2)如果有触礁的危险,这艘海轮在![]() 处改变航向为东偏南
处改变航向为东偏南![]() (
(![]() )方向航行,求
)方向航行,求![]() 的最小值.
的最小值.
附: ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2﹣4ax+b(a>0)在区间[0,1]上有最大值1和最小值﹣2.
(1)求a,b的值;
(2)若不等式f(x)≥mx在x∈(0,+∞)上恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax+xlnx(a∈R)
(1)若函数f(x)在区间[e,+∞)上为增函数,求a的取值范围;
(2)当a=1且k∈Z时,不等式k(x﹣1)<f(x)在x∈(1,+∞)上恒成立,求k的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(cosα﹣
=(cosα﹣ ![]() ,﹣1),
,﹣1), ![]() =(sinα,1),
=(sinα,1), ![]() 与
与 ![]() 为共线向量,且α∈[﹣
为共线向量,且α∈[﹣ ![]() ,0].
,0].
(1)求sinα+cosα的值;
(2)求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司今年年初用25万元引进一种新的设备,投入设备后每年收益为21万元.该公司第n年需要付出设备的维修和工人工资等费用an的信息如图. 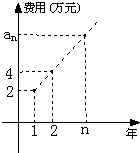
(1)求an;
(2)引进这种设备后,第几年后该公司开始获利;
(3)这种设备使用多少年,该公司的年平均获利最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex+ae﹣x , 若f′(x)≥2 ![]() 恒成立,则a的取值范围为( )
恒成立,则a的取值范围为( )
A.[3,+∞)
B.(0,3]
C.[﹣3,0)
D.(﹣∞,﹣3]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com