
【题目】过曲线y=x2(x≥0)上某一点A作一切线l,使之与曲线以及x轴所围成的图形的面积为 ![]() ,试求:
,试求:
(1)切点A的坐标;
(2)过切点A的切线l的方程.
【答案】
(1)解:设点A的坐标为(a,a2),过点A的切线的斜率为k=y'|x=a=2a,
故过点A的切线l的方程为y﹣a2=2a(x﹣a),即y=2ax﹣a2,令y=0,得 ![]() ,
,
则 ![]() ,
, ![]() ,
,
∴ ![]()
∴a=1
∴切点A的坐标为(1,1)
(2)解:∵直线的斜率k=2×1=2,
且过点(1,1)
∴直线方程为y=2x﹣1
【解析】(1)欲求切点A的坐标,设点A的坐标为(a,a2),只须在切点处的切线方程,故先利用导数求出在切点处的导函数值,再结合导数的几何意义即可求出切线的斜率从而得到切线的方程进而求得面积的表达式.最后建立关于a的方程解之即得.(2)欲求过切点A的切线l的方程,只须求出其斜率的值即可,由(1)中求得的导数值即可求出切线的斜率.从而问题解决.


 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案科目:高中数学 来源: 题型:
【题目】已知 ![]() 的展开式的系数和比(3x﹣1)n的展开式的系数和大992,求(2x﹣
的展开式的系数和比(3x﹣1)n的展开式的系数和大992,求(2x﹣ ![]() )2n的展开式中:
)2n的展开式中:
(1)二项式系数最大的项;
(2)系数的绝对值最大的项.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正四棱锥![]() 中,已知异面直线
中,已知异面直线![]() 与
与![]() 所成的角为
所成的角为![]() ,给出下面三个命题:
,给出下面三个命题:
![]() :若
:若![]() ,则此四棱锥的侧面积为
,则此四棱锥的侧面积为![]() ;
;
![]() :若
:若![]() 分别为
分别为![]() 的中点,则
的中点,则![]() 平面
平面![]() ;
;
![]() :若
:若![]() 都在球
都在球![]() 的表面上,则球
的表面上,则球![]() 的表面积是四边形
的表面积是四边形![]() 面积的
面积的![]() 倍.
倍.
在下列命题中,为真命题的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正四棱锥S﹣ABCD中,E,M,N分别是BC,CD,SC的中点,动点P在线段MN上运动时,下列四个结论:①EP⊥AC;②EP∥BD;③EP∥面SBD;④EP⊥面SAC.中恒成立的为( ) 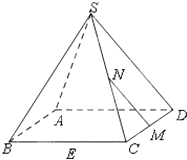
A.①③
B.③④
C.①②
D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ex﹣ax﹣2.
(1)求f(x)的单调区间;
(2)若a=1,k为整数,且当x>0时,(x﹣k)f′(x)+x+1>0,求k的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市随机抽取一年内100 天的空气质量指数(AQI)的监测数据,结果统计如表:
API | [0,50] | (50,100] | (100,150] | (150,200] | (200,300] | >300 |
空气质量 | 优 | 良 | 轻度污染 | 轻度污染 | 中度污染 | 重度污染 |
天数 | 6 | 14 | 18 | 27 | 20 | 15 |
(1)若本次抽取的样本数据有30 天是在供暖季,其中有8 天为严重污染.根据提
供的统计数据,完成下面的2×2 列联表,并判断是否有95%的把握认为“该城市本年的
空气严重污染与供暖有关”?
非重度污染 | 严重污染 | 合计 | |
供暖季 | |||
非供暖季 | |||
合计 | 100 |
(2)已知某企业每天的经济损失y(单位:元)与空气质量指数x 的关系式为y=  试估计该企业一个月(按30 天计算)的经济损失的数学期望.
试估计该企业一个月(按30 天计算)的经济损失的数学期望.
参考公式:K2= ![]()
P(K2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD的底面ABCD是平行四边形,PB⊥面ABCD,BA=BD= ![]() ,AD=2,E,F分别是棱AD,PC的中点.
,AD=2,E,F分别是棱AD,PC的中点. 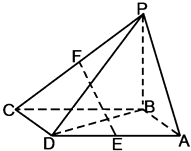
(1)证明:EF∥平面PAB;
(2)若二面角P﹣AD﹣B为60°,求直线EF与平面PBC所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com