考点:直线与圆锥曲线的综合问题
专题:圆锥曲线的定义、性质与方程,圆锥曲线中的最值与范围问题
分析:(Ⅰ)根据抛物线的定义,利用条件|PF|=3,求建立方程关系即可求点M的坐标;
(Ⅱ)设直线AB的方程为y=kx+m,利用直线和抛物线联立结合弦长公式公式以及点到直线的距离公式,利用导数即可求出三角形面积的最值.
解答:
解:(Ⅰ)由题意知焦点F(0,1),准线方程为y=-1,
设P(x
0,y
0),由抛物线的定义可知|PF|=y
0+1,解得y
0=2,
∴x
0=
±2,即P(2
,2)或P(-2
,2),
由
=3
,得M(-
,
)或M(
,
).
(Ⅱ)设直线AB的方程为y=kx+m,A(x
1,y
1),B(x
2,y
2),
由
得x
2-4kx-4m=0,
于是△=16k
2+16m>0,x
1+x
2=4k,x
1x
2=-4m,
即AB的中点M的坐标为(2k,2k
2+m)
由
=3
,得(-x
0,1-y
0)=3(2k,2k
2+m-1),
解得
,由
=4y0,得k
2=-
m+
,
由△>0,k>0得
-<m≤,
又∵|AB|=4
•,
点F到直线AB的距离d=
,
∴S
△ABP=4S
△ABF=8|m-1|
•=,
设f(m)=3m
3-5m
2+m+1,(
-<m≤),
则f'(m)=9m
2-10m+1=0,解得m
1=
,m
2=1,
于是f(m)在(
-,)是增函数,在(
,1)上是减函数,在(1,
)上是增函数,
又f(
)=
>f(),
∴当m=
时,f(m)取得最大值
,此时k=
±,
∴△ABP面积的最大值为
.
点评:本题主要考查抛物线的几何性质,直线和抛物线的位置关系,三角形面积公式,平面向量等基础知识,同时也考查解析几何的基本思想方法和运算求解能力.运算量大,综合性强,难度较大.

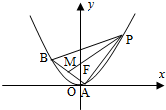 已知△ABP的三个顶点在抛物线C:x2=4y上,F为抛物线C的焦点,点M为AB的中点,
已知△ABP的三个顶点在抛物线C:x2=4y上,F为抛物线C的焦点,点M为AB的中点,

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案