
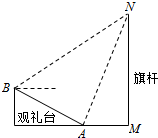
 2014年足球世界杯赛上举行升旗仪式.如图,在坡度为15°的观礼台上,某一列座位所在直线AB与旗杆所在直线MN共面,在该列的第一个座位A和最后一个座位B测得旗杆顶端N的仰角分别为60°和45°,若旗杆的高度为30米,则且座位A、B的距离为10($\sqrt{6}$-$\sqrt{2}$) 米.
2014年足球世界杯赛上举行升旗仪式.如图,在坡度为15°的观礼台上,某一列座位所在直线AB与旗杆所在直线MN共面,在该列的第一个座位A和最后一个座位B测得旗杆顶端N的仰角分别为60°和45°,若旗杆的高度为30米,则且座位A、B的距离为10($\sqrt{6}$-$\sqrt{2}$) 米. 分析 过B作BD∥AM交MN与D,由三角形的边角关系可得AN,进而在△ABN中由正弦定理可得.
解答 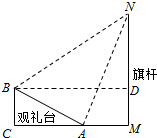 解:如图过B作BD∥AM交MN与D,
解:如图过B作BD∥AM交MN与D,
则由题意可得∠NAM=60°,∠NBD=45°,
∠ABD=∠CAB=15°,MN=30,
∴∠ABN=45°+15°=60°,∠ANB=45°-30°,
在△AMN中可得AN=$\frac{MN}{sin60°}$=$\frac{60}{\sqrt{3}}$,
在△ABN中$\frac{AB}{sin∠ANB}$=$\frac{AN}{sin∠ABN}$,
∴AB=$\frac{60}{\sqrt{3}}$×sin(45°-30°)÷$\frac{\sqrt{3}}{2}$=10($\sqrt{6}$-$\sqrt{2}$)
故答案为:10($\sqrt{6}$-$\sqrt{2}$)
点评 本题考查解三角形的实际应用,涉及正弦定理的应用和三角形的边角关系,属中档题.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
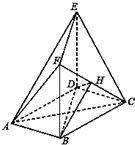 如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,H是CF的中点.
如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,H是CF的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
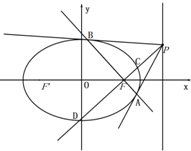 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,以原点为圆心,以椭圆的短半轴为半径的圆与直线x-y+$\sqrt{6}$=0相切.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,以原点为圆心,以椭圆的短半轴为半径的圆与直线x-y+$\sqrt{6}$=0相切.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com