
分析 设直线方程为y=k(x+3)或x=-3,根据直线l被圆圆x2+(y+2)2=25所截得的弦长为8,可得圆心到直线的距离为3,利用点到直线的距离公式确定k值,验证x=-3是否符合题意.
解答 解:设直线方程为y=k(x+3)或x=-3,
∵圆心坐标为(0,-2),圆的半径为5,
∴圆心到直线的距离d=$\sqrt{25-16}$=3,
∴$\frac{|3k+2|}{\sqrt{1+{k}^{2}}}$=3,
∴k=$\frac{5}{12}$,∴直线方程为y=$\frac{5}{12}$(x+3),即5x-12y+15=0;
直线x=-3,圆心到直线的距离d=|-3|=3,符合题意,
故答案为:x=-3或5x-12y+15=0.
点评 本题考查了待定系数法求直线方程,考查了直线与圆相交的相交弦长公式,注意不要漏掉x=-3.


 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $f(0)<f(\frac{3}{5})<f(-\frac{1}{2})$ | B. | $f(0)<f(-\frac{1}{2})<f(\frac{3}{5})$ | C. | $f(\frac{3}{5})<f(-\frac{1}{2})<f(0)$ | D. | $f(-\frac{1}{2})<f(0)<f(\frac{3}{5})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | $\frac{4}{3}$ | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
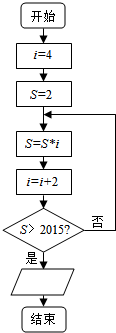
| A. | 输出i-2 | B. | 输出i-1 | C. | 输出i | D. | 输出i+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
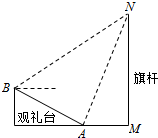 2014年足球世界杯赛上举行升旗仪式.如图,在坡度为15°的观礼台上,某一列座位所在直线AB与旗杆所在直线MN共面,在该列的第一个座位A和最后一个座位B测得旗杆顶端N的仰角分别为60°和45°,若旗杆的高度为30米,则且座位A、B的距离为10($\sqrt{6}$-$\sqrt{2}$) 米.
2014年足球世界杯赛上举行升旗仪式.如图,在坡度为15°的观礼台上,某一列座位所在直线AB与旗杆所在直线MN共面,在该列的第一个座位A和最后一个座位B测得旗杆顶端N的仰角分别为60°和45°,若旗杆的高度为30米,则且座位A、B的距离为10($\sqrt{6}$-$\sqrt{2}$) 米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com