练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知数列{an}的前n项和Sn＝2n2＋2n，数列{bn}的前n项和Tn＝2－bn.求数列{an}与{bn}的通项公式．


    解：∵当n≥2时，an＝Sn－Sn－1＝(2n2＋2n)－[2(n－1)2＋2(n－1)]＝4n，

    当n＝1时，a1＝S1＝4也适合，

    ∴{an}的通项公式是an＝4n(n∈N*)．

    ∵Tn＝2－bn，∴当n＝1时，b1＝2－b1，b1＝1.

    当n≥2时，bn＝Tn－Tn－1＝(2－bn)－(2－bn－1)，

    ∴2bn＝bn－1，

    ∴数列{bn}是公比为，首项为1的等比数列．

    ∴bn＝n－1.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知向量a＝(3,1)，b＝(1,3)，c＝(k,7)，若(a－c)∥b，则k＝(　　)

    A．3                                    B．0 

    C．5                                    D．－5

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    下列四个命题：

    ①对立事件一定是互斥事件；

    ②若A，B为两个事件，则P(A∪B)＝P(A)＋P(B)；

    ③若事件A，B，C彼此互斥，则P(A)＋P(B)＋P(C)＝1；

    ④若事件A，B满足P(A)＋P(B)＝1，则A，B是对立事件．

    其中错误命题的个数是(　　)．

    A．0                                                     B．1 

    C．2                                                     D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    有编号为A1，A2，…，A10的10个零件，测量其直径(单位：cm)，得到下面数据：

    编号

    A1

    A2

    A3

    A4

    A5

    A6

    A7

    A8

    A9

    A10

    直径

    1.51

    1.49

    1.49

    1.51

    1.49

    1.51

    1.47

    1.46

    1.53

    1.47

    其中直径在区间[1.48,1.52]内的零件为一等品．

    (Ⅰ)从上述10个零件中，随机抽取一个，求这个零件为一等品的概率；

    (Ⅱ)从一等品零件中，随机抽取2个．

    ①用零件的编号列出所有可能的抽取结果；

    ②求这2个零件直径相等的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    古希腊著名的毕达哥拉斯学派把1、3、6、10……这样的数称为“三角形数”，而把1、4、9、16……这样的数称为“正方形数”．如图中可以发现，任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和，下列等式中，符合这一规律的表达式为(　　)

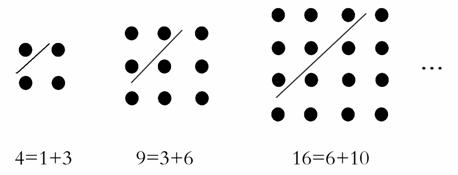
    ①13＝3＋10；②25＝9＋16；③36＝15＋21；④49＝18＋31；⑤64＝28＋36

    A．③⑤  B．②④⑤  C．②③④  D．①②③⑤

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知{an}为等差数列，若a3＋a4＋a8＝9，则S9＝(　　)

    A．24                                   B．27 

    C．15                                   D．54

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    现有一根n节的竹竿，自上而下每节的长度依次构成等差数列，最上面一节长为10 cm，最下面的三节长度之和为114 cm，第6节的长度是首节与末节长度的等比中项，则n＝________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知数列{an}、{bn}分别是首项均为2，各项均为正数的等比数列和等差数列，且b2＝4a2，a2b3＝6.

    (1)求数列{an}、{bn}的通项公式；

    (2)求使abn<0.001成立的最小的n值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知直线l：kx－y＋1＋2k＝0(k∈R)．

    (1)证明：直线l过定点；

    (2)若直线不经过第四象限，求k的取值范围；

    (3)若直线l交x轴负半轴于A，交y轴正半轴于B，△AOB的面积为S，求S的最小值并求此时直线l的方程．

    查看答案和解析>>

    同步练习册答案