
【题目】已知函数![]() .
.
(Ⅰ)当![]() 时,解不等式
时,解不等式![]() ;
;
(Ⅱ)若![]() ,对任意
,对任意![]() 都有
都有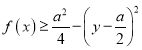 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ) (∞,5)∪(1,+∞);(Ⅱ)(0,6]
【解析】
(Ⅰ)由题知当a=1时,不等式![]() 等价于|x+3|+|x+1|>6,根据绝对值的几何意义能求出不等式
等价于|x+3|+|x+1|>6,根据绝对值的几何意义能求出不等式![]() 的解集.
的解集.
(Ⅱ) 由![]() ,对任意
,对任意![]() 都有
都有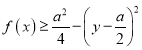 ,只需f(x)的最小值大于等于
,只需f(x)的最小值大于等于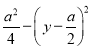 的最大值即可,转化成函数最值问题建立不等关系式,由此能求出a的取值范围.
的最大值即可,转化成函数最值问题建立不等关系式,由此能求出a的取值范围.
(Ⅰ)∵函数![]() ,
,
∴当a=1时,不等式![]() 等价于|x+3|+|x+1|>6,
等价于|x+3|+|x+1|>6,
根据绝对值的几何意义:
|x+3|+|x+1|>6可以看作数轴上的点x到点3和点1的距离之和大于6,
则点x到点3和点1的中点O的距离大于3即可,
∴点x在5或其左边及1或其右边,
即x<5或x>1.
∴不等式![]() 的解集为(∞,5)∪(1,+∞).
的解集为(∞,5)∪(1,+∞).
(Ⅱ) ∵![]() ,对任意
,对任意![]() 都有
都有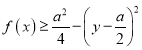 ,
,
只需f(x)的最小值大于等于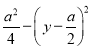 的最大值即可.
的最大值即可.
由![]() 可得,
可得,
![]() ,
,
设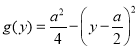 ,根据二次函数性质,
,根据二次函数性质,
![]() ,
,
∴![]() ,
,
解得![]() ,
,
又![]() ,
,
∴![]()
∴a的取值范围是(0,6].


科目:高中数学 来源: 题型:
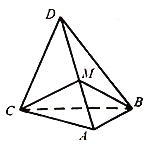
【题目】如图,在三棱锥![]() 中,
中,![]() 为等边三角形,
为等边三角形,![]() ,
,![]() 面积是
面积是![]() 面积的两倍,点
面积的两倍,点![]() 在侧棱
在侧棱![]() 上.
上.
(1)若![]() ,证明:平面
,证明:平面![]() 平面
平面![]() ;
;
(2)若二面角![]() 的大小为
的大小为![]() ,且
,且![]() 为
为![]() 的中点,求直线
的中点,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为调查高二年级学生的身高情况,按随机抽样的方法抽取80名学生,得到男生身高情况的频率分布直方图(图(1))和女生身高情况的频率分布直方图(图(2)).已知图(1)中身高(单位:![]() )在
)在![]() 内的男生人数有16人.
内的男生人数有16人.
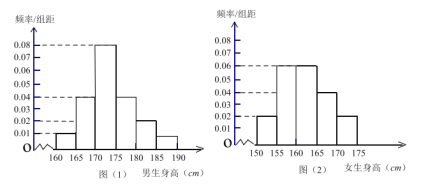
(Ⅰ)求在抽取的学生中,男女生各有多少人?
(Ⅱ)根据频率分布直方图,完成下列的![]() 列联表,并判断能有多大(百分之几)的把握认为“身高与性别有关”?
列联表,并判断能有多大(百分之几)的把握认为“身高与性别有关”?
|
| 总计 | |
男生人数 | |||
女生人数 | |||
总计 |
附:参考公式和临界值表:
 ,
,
| 5.024 | 6.635 | 7.879 | 10.828 |
| 0.025 | 0.010 | 0.005 | 0.001 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】石嘴山市第三中学高三年级统计学生的最近20次数学周测成绩(满分150分),现有甲乙两位同学的20次成绩如茎叶图所示:

(1)根据茎叶图求甲乙两位同学成绩的中位数,并将同学乙的成绩的频率分布直方图填充完整;
(2)根据茎叶图比较甲乙两位同学数学成绩的平均值及稳定程度(不要求计算出具体值,给出结论即可);
(3)现从甲乙两位同学的不低于140分的成绩中任意选出2个成绩,记事件![]() 为“其中2个成绩分别属于不同的同学”,求事件
为“其中2个成绩分别属于不同的同学”,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从1到9的九个数字中取三个偶数四个奇数,试问:
(1)能组成多少个没有重复数字的七位数?
(2)上述七位数中三个偶数排在一起的有几个?
(3)在(1)中的七位数中,偶数排在一起、奇数也排在一起的有几个?
(4)在(1)中任意两偶数都不相邻的七位数有几个?
查看答案和解析>>
科目:高中数学 来源: 题型:
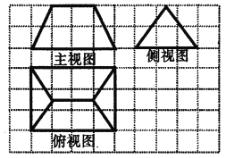
【题目】《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高二丈,问:积几何?”其意思为:“今有底面为矩形的屋脊状的锲体,下底面宽3丈,长4丈,上棱长2丈,高2丈,问:它的体积是多少?”(已知1丈为10尺)该锲体的三视图如图所示,则该锲体的体积为( )
A. 12000立方尺B. 11000立方尺
C. 10000立方尺D. 9000立方尺
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+ax﹣1(a∈R).
(Ⅰ)当a=1时,求f(x)>0的解集;
(Ⅱ)对于任意x∈R,不等式f(x)<0恒成立,求a的取值范围;
(Ⅲ)求关于x的不等式f(x)<0的解集.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com