Question

8．已知m∈R，函数f（x）=$\left\{\begin{array}{l}|2x+1|，x＜1\\ ln（x-1），x＞1\end{array}$，g（x）=x²-2x+2m²-1，若函数y=f（g（x））-m有6个零点则实数m的取值范围是$（0，\frac{3}{4}）$．

Answer 1

分析 令g（x）=t，由题意画出函数y=f（t）的图象，利用y=f（t）与y=m的图象最多有3个零点，可知要使函数y=f（g（x））-m有6个零点，则t=x²-2x+2m²-1中每一个t的值对应2个x的值，则t的值不能取最小值，求出y=f（t）与y=m交点横坐标的最小值，由其大于2m²-2，结合0＜m＜3求得实数m的取值范围．

解答 解：函数f（x）=$\left\{\begin{array}{l}|2x+1|，x＜1\\ ln（x-1），x＞1\end{array}$ 的图象如图所示，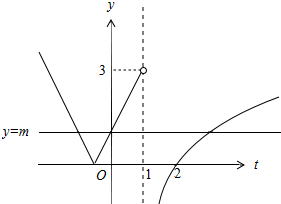

令g（x）=t，y=f（t）与y=m的图象最多有3个零点，
当有3个零点，则0＜m＜3，从左到右交点的横坐标依次t₁＜t₂＜t₃，
由于函数y=f（g（x））-m有6个零点，t=x²-2x+2m²-1，
则每一个t的值对应2个x的值，则t的值不能取最小值，
函数t=x²-2x+2m²-1的对称轴x=1，则t的最小值为1-2+2m²-1=2m²-2，
由图可知，2t₁+1=-m，则${t}_{1}=\frac{-m-1}{2}$，
由于t₁是交点横坐标中最小的，满足$\frac{-m-1}{2}$＞2m²-2①，
又0＜m＜3②，
联立①②得0＜m＜$\frac{3}{4}$．
∴实数m的取值范围是（0，$\frac{3}{4}$）．
故答案为：$（0，\frac{3}{4}）$．

点评 本题考查根的存在性及根的个数判断，考查数形结合的解题思想方法和数学转化思想方法，属于有一定难度题目．