
分析 根据原点坐标和已知的C点坐标,求出直线OC的斜率;根据平行四边形的两条对边平行得到AB平行于OC,又CD垂直与AB,所以CD垂直与OC,由(1)求出的直线OC的斜率,根据两直线垂直时斜率乘积为-1,求出CD所在直线的斜率,然后根据求出的斜率和点C的坐标写出直线CD的方程即可.
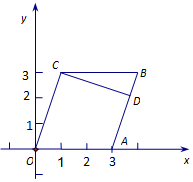
解答 解:因为点O(0,0),点C(1,3),
所以OC所在直线的斜率为${k_{OC}}=\frac{3-0}{1-0}=3$.(2分),
在平行四边形OABC中,AB∥OC,因为CD⊥AB,所以CD⊥OC.
所以 CD所在直线的斜率为${k_{CD}}=-\frac{1}{3}$.(6分)
所以CD所在直线方程为$y-3=-\frac{1}{3}(x-1)$,即x+3y-10=0.(10分)
点评 此题考查学生会根据两点的坐标求出过两点直线方程的斜率,掌握两直线平行时斜率所满足的条件,会根据一点和斜率写出直线的点斜式方程,是一道综合题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

| $\overline x$ | $\overline y$ | $\overline w$ | ${\sum_{i=1}^8{({x_i}-\overline x)}^2}$ | ${\sum_{i=1}^8{({w_i}-\overline w)}^2}$ | $\sum_{i=1}^8{({x_i}-\overline x)}({y_i}-\overline y)$ | $\sum_{i=1}^8{({w_i}-\overline w)}({y_i}-\overline y)$ |
| 46.6 | 56.3 | 6.8 | 289.8 | 1.6 | 1469 | 108.8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 14π | B. | 16π | C. | 13π | D. | 15π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
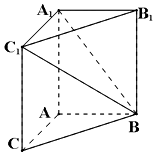 如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.
如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com