
【题目】已知椭圆E: ![]() 的左、右焦点分别为F1 , F2 , 左、右顶点分别为A,B.以F1F2为直径的圆O过椭圆E的上顶点D,直线DB与圆O相交得到的弦长为
的左、右焦点分别为F1 , F2 , 左、右顶点分别为A,B.以F1F2为直径的圆O过椭圆E的上顶点D,直线DB与圆O相交得到的弦长为 ![]() .设点P(a,t)(t≠0),连接PA交椭圆于点C,坐标原点为O.
.设点P(a,t)(t≠0),连接PA交椭圆于点C,坐标原点为O.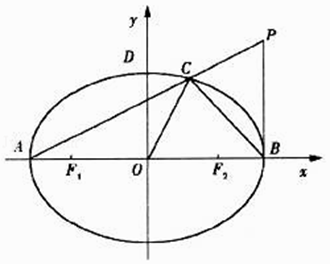
(I)求椭圆E的方程;
(II)若三角形ABC的面积不大于四边形OBPC的面积,求|t|的最小值.
【答案】解:(Ⅰ)因为以F1,F2为直径的圆O过点D,所以b=c,则圆O的方程为x2+y2=b2,
又a2=b2+c2,所以 ![]() ,直线DB的方程为
,直线DB的方程为 ![]() ,直线DB与圆O相交得到的弦长为
,直线DB与圆O相交得到的弦长为 ![]() ,
,
则 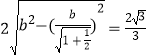 ,所以b=1,
,所以b=1, ![]() ,
,
所以椭圆E的方程为 ![]() .
.
(Ⅱ)由已知得: ![]() ,b=1,椭圆方程为
,b=1,椭圆方程为 ![]() ,
,
设直线PA的方程为 ![]() ,由
,由 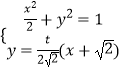
整理得 ![]() ,
,
解得: ![]() ,
, ![]() ,则点C的坐标是
,则点C的坐标是 ![]() ,
,
故直线BC的斜率为 ![]() ,由于直线OP的斜率为
,由于直线OP的斜率为 ![]() ,
,
所以kBCkOP=﹣1,所以OP⊥BC.
所以 ![]() ,
, ![]() ,所以
,所以 ![]() ,
,
整理得2+t2≥4, ![]() ,所以
,所以 ![]()
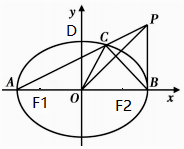
【解析】(Ⅰ)由题意可知:b=c,则 ![]() ,则直线DB的方程为
,则直线DB的方程为 ![]() ,由题意可知
,由题意可知 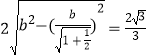 ,即可求得b及a的值,求得椭圆方程;(2)设直线PA的方程为
,即可求得b及a的值,求得椭圆方程;(2)设直线PA的方程为 ![]() ,代入椭圆方程,求得C点坐标,直线BC的斜率为
,代入椭圆方程,求得C点坐标,直线BC的斜率为 ![]() ,由于直线OP的斜率为
,由于直线OP的斜率为 ![]() ,可得OP⊥BC,分别求得三角形ABC的面积及四边形OBPC的面积由
,可得OP⊥BC,分别求得三角形ABC的面积及四边形OBPC的面积由 ![]() ,即可求得丨t丨取值范围,即可求得|t|的最小值.
,即可求得丨t丨取值范围,即可求得|t|的最小值.


 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:
【题目】我国古代数学名著《九章算术》的论割圆术中有:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣.”它体现了一种无限与有限的转化过程.比如在表达式1+ ![]() 中“…”即代表无数次重复,但原式却是个定值,它可以通过方程1+
中“…”即代表无数次重复,但原式却是个定值,它可以通过方程1+ ![]() =x求得x=
=x求得x= ![]() .类比上述过程,则
.类比上述过程,则 ![]() =( )
=( )
A.3
B.![]()
C.6
D.2 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人组成“星队”参加猜成语活动,每轮活动由甲、乙各猜一个成语,在一轮活动中,如果两人都猜对,则“星队”得3分;如果只有一个人猜对,则“星队”得1分;如果两人都没猜对,则“星队”得0分.已知甲每轮猜对的概率是 ![]() ,乙每轮猜对的概率是
,乙每轮猜对的概率是 ![]() ;每轮活动中甲、乙猜对与否互不影响.各轮结果亦互不影响.假设“星队”参加两轮活动,求:
;每轮活动中甲、乙猜对与否互不影响.各轮结果亦互不影响.假设“星队”参加两轮活动,求:
(I)“星队”至少猜对3个成语的概率;
(II)“星队”两轮得分之和为X的分布列和数学期望EX.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体ABCD﹣A1B1C1D1的棱长为1,线段B1D1上有两个动点E、F,且EF=![]() ,则下列结论中正确的序号是_____.
,则下列结论中正确的序号是_____.

①AC⊥BE ②EF∥平面ABCD ③△AEF的面积与△BEF的面积相等.④三棱锥A﹣BEF的体积为定值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且满足12Sn﹣36=3n2+8n,数列{log3bn}为等差数列,且b1=3,b3=27.
(Ⅰ)求数列{an}与{bn}的通项公式;
(Ⅱ)令cn=(﹣1)n ![]() ,求数列{cn}的前n项和Tn .
,求数列{cn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,D是A1B1的中点. 
(1)求证:A1C∥平面BDC1;
(2)若AB⊥AC,且AB=AC= ![]() AA1 , 求二面角A﹣BD﹣C1的余弦值.
AA1 , 求二面角A﹣BD﹣C1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,g(x)=﹣2xln(1+
,g(x)=﹣2xln(1+ ![]() )﹣lnf(x).
)﹣lnf(x).
(Ⅰ)讨论函数f(x)的单调性;
(Ⅱ)当a=0时,函数g(x)在定义域内是否存在零点?如果存在,求出该零点;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com