
分析 作出f(x)=$\left\{\begin{array}{l}{sinπx,\;\;\;x∈[0,2]}\\{\frac{1}{2}f(x-2),x∈(2,+∞)}\end{array}\right.$的图象,分别利用函数的性质进行判断即可.
解答 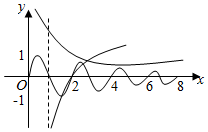 解:f(x)=$\left\{\begin{array}{l}{sinπx,\;\;\;x∈[0,2]}\\{\frac{1}{2}f(x-2),x∈(2,+∞)}\end{array}\right.$的图象如图所示:
解:f(x)=$\left\{\begin{array}{l}{sinπx,\;\;\;x∈[0,2]}\\{\frac{1}{2}f(x-2),x∈(2,+∞)}\end{array}\right.$的图象如图所示:
①∵f(x)的最大值为1,最小值为-1,
∴任取x1、x2∈[0,+∞),都有|f(x1)-f(x2)|≤2恒成立,故①正确;
②函数在区间[4,5]上的单调性和[0,1]上的单调性相同,则函数y=f(x)在区间[4,5]上不单调;故②错误;
③f($\frac{1}{2}$)=2f($\frac{1}{2}$+2)=4f($\frac{1}{2}$+4)=6f($\frac{1}{2}$+6)≠8f($\frac{1}{2}$+8),故不正确;故③错误,
④如图所示,函数y=f(x)-ln(x-1)有3个零点;故④正确,
⑤当1≤x≤2时,函数f(x)关于x=$\frac{3}{2}$对称,若关于x的方程f(x)=m(m<0)有且只有两个不同实根x1,x2,
则$\frac{{x}_{1}+{x}_{2}}{2}$=$\frac{3}{2}$,则x1+x2=3成立,故⑤正确,
故答案为:①④⑤.
点评 本题主要考查命题的真假判断,涉及函数的性质,利用分段函数的表达式,作出函数的图象,利用数形结合是解决本题的关键.综合性较强,有一定的难度.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,在四棱锥P-ABCD中,AB⊥平面PAD,AB∥CD,PD=AD,E是PB中点,F是DC上的点,且$DF=\frac{1}{2}AB,PH$为△PAD中AD边上的高.
如图所示,在四棱锥P-ABCD中,AB⊥平面PAD,AB∥CD,PD=AD,E是PB中点,F是DC上的点,且$DF=\frac{1}{2}AB,PH$为△PAD中AD边上的高.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
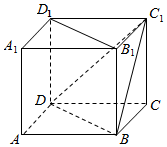 如图,ABCD-A1B1C1D1为正方体.
如图,ABCD-A1B1C1D1为正方体.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,在正方体ABCD-A1B1C1D1中,M是AB上一点,N是A1C的中点,MN⊥平面A1DC.
如图所示,在正方体ABCD-A1B1C1D1中,M是AB上一点,N是A1C的中点,MN⊥平面A1DC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com