Question

19．在四面体A-BCD中，有两条棱的长为a（a＞0），其余棱的长度为1．
（1）若a=$\frac{3}{2}$，且AB=AC=$\frac{3}{2}$，求二面角A-BC-D的余弦值；
（2）求a的取值范围，使得这样的四面体是存在的．

Answer 1

分析 （1）由题意画出图形，作出二面角的平面角，利用余弦定理得答案；
（2）分两条长为a的棱相交与两条长为a的棱互为对棱分析，结合运动思想与极限思想求得每一种情况的a的范围，最后取并集得答案．

解答 解：（1）如图，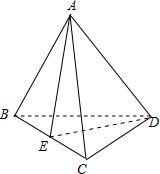
过A作AE⊥BC，垂足为E，连接DE，则∠AED为二面角A-BC-D的平面角，
在等边三角形BCD中，∵BC=CD=BD=1，∴DE=$\sqrt{{1}^{2}-（\frac{1}{2}）^{2}}=\frac{\sqrt{3}}{2}$，
在等腰三角形ABC中，∵AB=AC=$\frac{3}{2}$，BC=1，∴AE=$\sqrt{（\frac{3}{2}）^{2}-（\frac{1}{2}）^{2}}=\sqrt{2}$．
在△AED中，由余弦定理得cos∠AED=$\frac{（\frac{\sqrt{3}}{2}）^{2}+（\sqrt{2}）^{2}-{1}^{2}}{2×\frac{\sqrt{3}}{2}×\sqrt{2}}=\frac{7\sqrt{6}}{24}$；
（2）当两条长为a的棱相交时，不妨设AB=AC=a，AD=BD=CD=BC=1，
∵面ABC与平面BCD重合且A，D在BC异侧时，AE=$1-\frac{\sqrt{3}}{2}$，此时AB=AC=$\sqrt{（\frac{1}{2}）^{2}+（1-\frac{\sqrt{3}}{2}）^{2}}=\sqrt{2-\sqrt{3}}=\frac{\sqrt{6}-\sqrt{2}}{2}$，
面ABC与平面BCD重合且A，D在BC同侧时，AE=1+$\frac{\sqrt{3}}{2}$，此时AB=AC=$\sqrt{（\frac{1}{2}）^{2}+（1+\frac{\sqrt{3}}{2}）^{2}}=\sqrt{2+\sqrt{3}}=\frac{\sqrt{6}+\sqrt{2}}{2}$．
∴$\frac{\sqrt{6}-\sqrt{2}}{2}＜a＜\frac{\sqrt{6}+\sqrt{2}}{2}$；
当两条长为a的棱互为对棱时，不妨设BC=AD=a，AB=AC=BD=CD=1，BC，AD可以无限趋近于0，
当ABCD为平面四边形时a=$\sqrt{2}$，
∴0$＜a＜\sqrt{2}$．
综上，若四面体存在，则0＜a$＜1+\frac{\sqrt{3}}{2}$．

点评 本题考查棱锥的结构特征，考查了二面角的平面角的求法，解答（2）的关键是运动思想与极限思想的应用，是中档题．