
ЎҫМвДҝЎҝ·Ё№ъКэС§јТЕУјУКЗёцПІ»¶іФГж°ьөДИЛЈ¬ЛыГҝМм¶ј»б№әВтТ»ёцГж°ьЈ¬Гж°ьКҰЙщіЖЧФјәіцКЫөДГҝёцГж°ьөДЖҪҫщЦКБҝКЗ1000![]() Ј¬ЙППВёЎ¶ҜІ»і¬№э50
Ј¬ЙППВёЎ¶ҜІ»і¬№э50![]() .Хвҫд»°УГКэС§УпСФАҙұнҙпҫНКЗЈәГҝёцГж°ьөДЦКБҝ·юҙУЖЪНыОӘ1000
.Хвҫд»°УГКэС§УпСФАҙұнҙпҫНКЗЈәГҝёцГж°ьөДЦКБҝ·юҙУЖЪНыОӘ1000![]() Ј¬ұкЧјІоОӘ50
Ј¬ұкЧјІоОӘ50![]() өДХэМ¬·ЦІј.
өДХэМ¬·ЦІј.
ЈЁ1Ј©јЩЙиГж°ьКҰөДЛө·ЁКЗХжКөөДЈ¬ҙУГж°ьКҰіцКЫөДГж°ьЦРИОИЎБҪёцЈ¬јЗИЎіцөДБҪёцГж°ьЦРЦКБҝҙуУЪ1000![]() өДёцКэОӘ
өДёцКэОӘ![]() Ј¬Зу
Ј¬Зу![]() өД·ЦІјБРәНКэС§ЖЪНыЈ»
өД·ЦІјБРәНКэС§ЖЪНыЈ»
ЈЁ2Ј©ЧчОӘТ»ёцЙЖУЪЛјҝјөДКэС§јТЈ¬ЕУјУАіГҝМм¶ј»бҪ«ВтАҙөДГж°ьіЖЦШІўјЗВјЈ¬25МмәуЈ¬өГөҪКэҫЭИзПВұнЈ¬ҫӯјЖЛг25ёцГж°ьЧЬЦКБҝОӘ24468![]() .ЕУјУАі№әВтөД25ёцГж°ьЦКБҝөДНіјЖКэҫЭЈЁөҘО»Јә
.ЕУјУАі№әВтөД25ёцГж°ьЦКБҝөДНіјЖКэҫЭЈЁөҘО»Јә![]() Ј©
Ј©
981 | 972 | 966 | 992 | 1010 | 1008 | 954 | 952 | 969 | 978 |
989 | 1001 | 1006 | 957 | 952 | 969 | 981 | 984 | 952 | 959 |
987 | 1006 | 1000 | 977 | 966 |
ҫЎ№ЬЙПКцКэҫЭ¶јВдФЪ![]() ЙПЈ¬ө«ЕУјУІЛ»№КЗИПОӘГж°ьКҰИц»СЈ¬ёщҫЭЛщёҪРЕПўЈ¬ҙУёЕВКҪЗ¶ИЛөГчАнУЙ
ЙПЈ¬ө«ЕУјУІЛ»№КЗИПОӘГж°ьКҰИц»СЈ¬ёщҫЭЛщёҪРЕПўЈ¬ҙУёЕВКҪЗ¶ИЛөГчАнУЙ
ёҪЈә
ўЩИф![]() Ј¬ҙУXөДИЎЦөЦРЛж»ъійИЎ25ёцКэҫЭЈ¬јЗХв25ёцКэҫЭөДЖҪҫщЦөОӘYЈ¬ФтУЙНіјЖС§ЦӘК¶ҝЙЦӘЈәЛж»ъұдБҝ
Ј¬ҙУXөДИЎЦөЦРЛж»ъійИЎ25ёцКэҫЭЈ¬јЗХв25ёцКэҫЭөДЖҪҫщЦөОӘYЈ¬ФтУЙНіјЖС§ЦӘК¶ҝЙЦӘЈәЛж»ъұдБҝ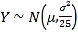
ўЪИф![]() Ј¬Фт
Ј¬Фт![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј»
Ј»
ўЫНЁіЈ°С·ўЙъёЕВКФЪ0.05ТФПВөДКВјюіЖОӘРЎёЕВККВјю.
Ўҫҙр°ёЎҝЈЁ1Ј©·ЦІјБРјыҪвОцЈ»ЖЪНыОӘ1ЈЁёцЈ©ЈЁ2Ј©ПкјыҪвОц
ЎҫҪвОцЎҝ
ЈЁ1Ј©УЙМвТвЦӘЈ¬![]() өДЛщУРҝЙДЬИЎЦөОӘ0Ј¬1Ј¬2.ҝЙЗуөГ
өДЛщУРҝЙДЬИЎЦөОӘ0Ј¬1Ј¬2.ҝЙЗуөГ![]() Ј»
Ј»![]() Ј»
Ј»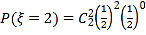 .ҙУ¶шҝЙЗуөГ
.ҙУ¶шҝЙЗуөГ![]() өД·ЦІјБРәНЖдКэС§ЖЪНы.
өД·ЦІјБРәНЖдКэС§ЖЪНы.
ЈЁ2Ј©јЗГж°ьКҰЦЖЧчөДГҝёцГж°ьөДЦКБҝОӘЛж»ъұдБҝX.јЩЙиГж°ьКҰГ»УРИц»СЈ¬Фт![]() .УЙёҪўЩЈ¬ҙУXөДИЎЦөЦРЛж»ъійИЎ25ёцКэҫЭЈ¬јЗХв25ёцКэҫЭөДЖҪҫщЦөОӘYЈ¬Фт
.УЙёҪўЩЈ¬ҙУXөДИЎЦөЦРЛж»ъійИЎ25ёцКэҫЭЈ¬јЗХв25ёцКэҫЭөДЖҪҫщЦөОӘYЈ¬Фт![]() .ҝЙЗуөГХв25ёцКэҫЭөДЖҪҫщЦөОӘ
.ҝЙЗуөГХв25ёцКэҫЭөДЖҪҫщЦөОӘ![]() Ј¬¶шУЙУЙёҪўЪКэҫЭЦӘЈ¬
Ј¬¶шУЙУЙёҪўЪКэҫЭЦӘЈ¬![]() Ј¬УЙёҪўЫЦӘЈ¬КВјюЎ°
Ј¬УЙёҪўЫЦӘЈ¬КВјюЎ°![]() ЎұОӘРЎёЕВККВјюЈ¬ҝЙөГҪбВЫ.
ЎұОӘРЎёЕВККВјюЈ¬ҝЙөГҪбВЫ.
ЈЁ1Ј©УЙМвТвЦӘЈ¬![]() өДЛщУРҝЙДЬИЎЦөОӘ0Ј¬1Ј¬2.
өДЛщУРҝЙДЬИЎЦөОӘ0Ј¬1Ј¬2.
![]() Ј»
Ј»![]() Ј»
Ј»
![]() .ЛщТФ
.ЛщТФ![]() өД·ЦІјБРОӘЈә
өД·ЦІјБРОӘЈә
| 0 | 1 | 2 |
P |
|
|
|
ЛщТФ![]() ЈЁёцЈ©.
ЈЁёцЈ©.
ЈЁ2Ј©јЗГж°ьКҰЦЖЧчөДГҝёцГж°ьөДЦКБҝОӘЛж»ъұдБҝX.
јЩЙиГж°ьКҰГ»УРИц»СЈ¬Фт![]() .
.
ёщҫЭёҪўЩЈ¬ҙУXөДИЎЦөЦРЛж»ъійИЎ25ёцКэҫЭЈ¬јЗХв25ёцКэҫЭөДЖҪҫщЦөОӘYЈ¬
Фт![]() .
.
ЕУјУАіјЗВјөД25ёцГж°ьЦКБҝЈ¬ПаөұУЪҙУXөДИЎЦөЦРЛж»ъійИЎБЛ25ёцКэҫЭЈ¬
Хв25ёцКэҫЭөДЖҪҫщЦөОӘ![]() Ј¬
Ј¬
УЙёҪўЪКэҫЭЦӘЈ¬![]() Ј¬
Ј¬
УЙёҪўЫЦӘЈ¬КВјюЎ°![]() ЎұОӘРЎёЕВККВјюЈ¬
ЎұОӘРЎёЕВККВјюЈ¬
ЛщТФЎ°јЩЙиГж°ьКҰГ»УРИц»СЎұУРОуЈ¬
ЛщТФЕУјУАіИПОӘГж°ьКҰИц»С.


 МмМмПтЙПТ»ұҫәГҫнПөБРҙр°ё
МмМмПтЙПТ»ұҫәГҫнПөБРҙр°ё РЎС§Йъ10·ЦЦУУҰУГМвПөБРҙр°ё
РЎС§Йъ10·ЦЦУУҰУГМвПөБРҙр°ё
| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
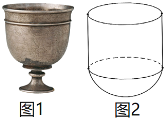
ЎҫМвДҝЎҝМЖіҜөДбчБФҫ°ПуёЎөсТшұӯИзНј1ЛщКҫ.ЖдёЎөсБЩДЎБЛ№ъ»ӯЎўЖб»жәНД№КТұЪ»ӯЈ¬МеПЦБЛ№ЕИЛөДЦЗ»ЫУл№ӨТХ.ЛьөДКўҫЖІҝ·ЦҝЙТФҪьЛЖөШҝҙЧчКЗ°лЗтУлФІЦщөДЧйәПМеЈЁјЩЙиДЪұЪұнГж№в»¬Ј¬әцВФұӯұЪәс¶ИЈ©Ј¬ИзНј2ЛщКҫ.ТСЦӘЗтөД°лҫ¶ОӘRЈ¬ҫЖұӯДЪұЪұнГж»эОӘ![]() ,ЙиҫЖұӯЙПІҝ·ЦЈЁФІЦщЈ©өДМе»эОӘ
,ЙиҫЖұӯЙПІҝ·ЦЈЁФІЦщЈ©өДМе»эОӘ![]() Ј¬ПВІҝ·ЦЈЁ°лЗтЈ©өДМе»эОӘ
Ј¬ПВІҝ·ЦЈЁ°лЗтЈ©өДМе»эОӘ![]() Ј¬Фт
Ј¬Фт![]() ЈЁ Ј©
ЈЁ Ј©
A.2B.![]() C.1D.
C.1D.![]()
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘәҜКэ![]()
(1)Иф![]() МЦВЫ
МЦВЫ![]() өДөҘөчРФ;
өДөҘөчРФ;
(2)өұ![]() Кұ,ИфәҜКэ
Кұ,ИфәҜКэ![]() Ул
Ул![]() өДНјПуУРЗТҪцУРТ»ёцҪ»өг
өДНјПуУРЗТҪцУРТ»ёцҪ»өг![]() ,Зу
,Зу![]() өДЦө(ЖдЦР
өДЦө(ЖдЦР![]() ұнКҫІ»і¬№э
ұнКҫІ»і¬№э![]() өДЧоҙуХыКэ,Из
өДЧоҙуХыКэ,Из![]() .
.
ІОҝјКэҫЭ:![]()
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
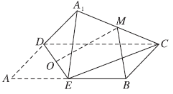
ЎҫМвДҝЎҝИзНјЈ¬ФЪҫШРО![]() ЦРЈ¬
ЦРЈ¬![]() ОӘұЯ
ОӘұЯ![]() өДЦРөгЈ¬Ҫ«
өДЦРөгЈ¬Ҫ«![]() СШЦұПЯ
СШЦұПЯ![]() ·ӯЧӘіЙ
·ӯЧӘіЙ![]() (
(![]() ЖҪГж
ЖҪГж![]() ).Иф
).Иф![]() ·ЦұрОӘПЯ¶О
·ЦұрОӘПЯ¶О![]() өДЦРөгЈ¬ФтФЪ
өДЦРөгЈ¬ФтФЪ![]() ·ӯЧӘ№эіМЦРЈ¬ПВБРЛө·ЁХэИ·өДКЗЈЁ Ј©
·ӯЧӘ№эіМЦРЈ¬ПВБРЛө·ЁХэИ·өДКЗЈЁ Ј©
A.УлЖҪГж![]() ҙ№ЦұөДЦұПЯұШУлЦұПЯ
ҙ№ЦұөДЦұПЯұШУлЦұПЯ![]() ҙ№Цұ
ҙ№Цұ
B.ТмГжЦұПЯ![]() Ул
Ул![]() ЛщіЙөДҪЗКЗ¶ЁЦө
ЛщіЙөДҪЗКЗ¶ЁЦө
C.Т»¶ЁҙжФЪДіёцО»ЦГЈ¬К№![]()
D.ИэАвЧ¶![]() НвҪУЗт°лҫ¶УлАв
НвҪУЗт°лҫ¶УлАв![]() өДіӨЦ®ұИОӘ¶ЁЦө
өДіӨЦ®ұИОӘ¶ЁЦө
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
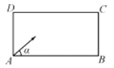
ЎҫМвДҝЎҝМЁЗтФЛ¶ҜТСУРОеЎўБщ°ЩДкөДАъК·Ј¬ІОУлХЯУГЗтёЛФЪМЁЙП»чЗт.ИфәН№вПЯТ»СщЈ¬МЁЗтФЪЗтМЁЙПЕцөҪХП°ӯОпәуТІЧсҙУ·ҙЙд¶ЁВЙИзНјЈ¬УРТ»ХЕіӨ·ҪРОЗтМЁABCDЈ¬![]() Ј¬ПЦҙУҪЗВдAСШҪЗ
Ј¬ПЦҙУҪЗВдAСШҪЗ![]() өД·ҪПт°СЗтҙтіцИҘЈ¬Зтҫӯ2ҙОЕцЧІЗтМЁДЪСШәуҪшИлҪЗВдCөДЗтҙьЦРЈ¬Фт
өД·ҪПт°СЗтҙтіцИҘЈ¬Зтҫӯ2ҙОЕцЧІЗтМЁДЪСШәуҪшИлҪЗВдCөДЗтҙьЦРЈ¬Фт![]() өДЦөОӘЈЁ Ј©
өДЦөОӘЈЁ Ј©
A.![]() B.
B.![]() C.1D.
C.1D.![]()
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝәҜКэf(x)=ex+asinxЈ¬xЎК(ЈӯҰРЈ¬+ЎЮ)Ј¬ПВБРЛө·ЁХэИ·өДКЗЈЁ Ј©
A.өұa=1КұЈ¬f(x)ФЪ(0Ј¬f(0))ҙҰөДЗРПЯ·ҪіМОӘ2xЈӯy+1=0
B.өұa=1КұЈ¬f(x)ҙжФЪОЁТ»ј«РЎЦөөгx0ЗТЈӯ1Јјf(x0)Јј0
C.¶ФИОТвaЈҫ0Ј¬f(x)ФЪ(ЈӯҰРЈ¬+ЎЮ)ЙПҫщҙжФЪБгөг
D.ҙжФЪaЈј0Ј¬f(x)ФЪ(ЈӯҰРЈ¬+ЎЮ)ЙПУРЗТЦ»УРТ»ёцБгөг
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
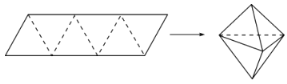
ЎҫМвДҝЎҝЕ©АъОеФВіхОеКЗ¶ЛОзҪЪЈ¬ГсјдУРіФфХЧУөДП°№ЯЈ¬фХЧУУЦіЖфХБЈЈ¬№ЕіЖҪЗКтЈ¬КЗ¶ЛОзҪЪҙујТ¶ј»бЖ·іўөДКіЖ·.ИзНјЈ¬ЖҪРРЛДұЯРОРОЧҙөДЦҪЖ¬КЗУЙБщёцұЯіӨОӘ2өДХэИэҪЗРО№№іЙөДЈ¬Ҫ«ЛьСШРйПЯХЫЖрАҙЈ¬ҝЙТФөГөҪИзНјЛщКҫфХЧУРОЧҙөДБщГжМеЈ¬ФтёГБщГжМеөДМе»эОӘ_________Ј»ИфёГБщГжМеДЪУРТ»ЗтЈ¬өұёГЗтМе»эЧоҙуКұЈ¬ЗтөДұнГж»эКЗ__________.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
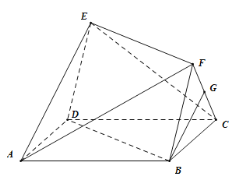
ЎҫМвДҝЎҝИзНјЈ¬ТСЦӘ¶аГжМе![]() Ј¬ЖдөЧГж
Ј¬ЖдөЧГж![]() ОӘҫШРОЈ¬ЛДұЯРО
ОӘҫШРОЈ¬ЛДұЯРО![]() ОӘЖҪРРЛДұЯРОЈ¬ЖҪГж
ОӘЖҪРРЛДұЯРОЈ¬ЖҪГж![]() ЖҪГж
ЖҪГж![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() КЗ
КЗ![]() өДЦРөг.
өДЦРөг.
ЈЁ1Ј©ЦӨГчЈә![]() ЖҪГж
ЖҪГж![]() Ј»
Ј»
ЈЁ2Ј©ЗуЦұПЯ![]() УлЖҪГж
УлЖҪГж![]() ЛщіЙҪЗөДУаПТЦө.
ЛщіЙҪЗөДУаПТЦө.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝЎ°¶юҪшЦЖЎұАҙФҙУЪОТ№ъ№ЕҙъөДЎ¶ТЧҫӯЎ·Ј¬ёГКйЦРУРБҪАаЧо»щұҫөД·ыәЕЈәЎ°©ӨЎұәНЎ°©Ғ©ҒЎұЈ¬ЖдЦРЎ°©ӨЎұФЪ¶юҪшЦЖЦРјЗЧчЎ°1ЎұЈ¬Ў°©Ғ©ҒЎұФЪ¶юҪшЦЖЦРјЗЧчЎ°0ЎұЈ®Из·ыәЕЎ°Ўұ¶ФУҰөД¶юҪшЦЖКэ011ЈЁ2Ј©»ҜОӘК®ҪшЦЖөДјЖЛгИзПВЈә011ЈЁ2Ј©ЈҪ0ЎБ22+1ЎБ21+1ЎБ20ЈҪ3ЈЁ10Ј©Ј®ИфҙУБҪАа·ыәЕЦРИОИЎ2ёц·ыәЕҪшРРЕЕБРЈ¬ФтөГөҪөД¶юҪшЦЖКэЛщ¶ФУҰөДК®ҪшЦЖКэҙуУЪ2өДёЕВКОӘЈЁ Ј©
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
Ійҝҙҙр°ёәНҪвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com