练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知抛物线y＝(m－1)x2＋(m－2)x－1(x∈R)．

    (1)当m为何值时，抛物线与x轴有两个交点？

    (2)若关于x的方程(m－1)x2＋(m－2)x－1＝0的两个不等实根的倒数平方和不大于2，求m的取值范围．


    解　(1)根据题意，m≠1且Δ>0，

    即Δ＝(m－2)2－4(m－1)(－1)>0，

    得m2>0，所以m≠1且m≠0.

    (2)在m≠0且m≠1的条件下，

    因为＋＝＝m－2，

    所以＋＝2－＝(m－2)2＋2(m－1)≤2.

    得m2－2m≤0，所以0≤m≤2.

    所以m的取值范围是{m|0<m<1或1<m≤2}．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知数列{an}的前n项和为Sn满足：Sn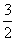＝an＋n－3.

    (1)求证：数列{an－1}是等比数列．

    (2)令cn＝log3(a1－1)＋log3(a2－1)＋…＋log3(an－1)，对任意n∈N*，是否存在正整数m，使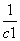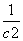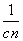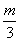＋＋…＋≥都成立？若存在，求出m的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    对于不等式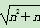<n＋1(n∈N*)，某同学用数学归纳法的证明过程如下：

    (1)当n＝1时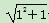，<1＋1，不等式成立．

    (2)假设当n＝k(k∈N*且k≥1)时，不等式成立，即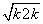<k＋1，则当n＝k＋1时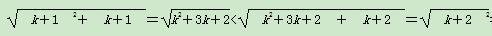，＝(k＋1)＋1，

    所以当n＝k＋1时，不等式成立，则上述证法(　　)

    A．过程全部正确

    B．n＝1验得不正确

    C．归纳假设不正确

    D．从n＝k到n＝k＋1的推理不正确

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    给出下列条件：①1<a<b；②0<a<b<1；③0<a<1<b.其中，能推出logb<loga<logab成立的条件的序号是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝－x2＋ax＋b2－b＋1(a∈R，b∈R)，对任意实数x都有f(1－x)＝f(1＋x)成立，当x∈[－1,1]时，f(x)>0恒成立，则b的取值范围是(　　)

    A．－1<b<0                              B．b>2

    C．b<－1或b>2                          D．不能确定

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知点(－3，－1)和点(4，－6)在直线3x－2y－a＝0的两侧，则a的取值范围为(　　)

    A．(－24,7)

    B．(－7,24)

    C．(－∞，－7)∪(24，＋∞)

    D．(－∞，－24)∪(7，＋∞)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若x，y满足则z＝x＋y的最小值为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     求函数y＝x(a－2x)(x>0，a为大于2x的常数)的最大值；

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    当a为任意实数时，直线(a－1)x－y＋a＋1＝0恒过定点C，则以C为圆心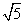，为半径的圆的方程为(　　)

    A．x2＋y2－2x＋4y＝0

    B．x2＋y2＋2x＋4y＝0

    C．x2＋y2＋2x－4y＝0

    D．x2＋y2－2x－4y＝0

     

    查看答案和解析>>

    同步练习册答案