练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    6．在一个2×2列联表中，由其数据计算得K2的观测值k=7.097，则这两个变量间有关系的可能性为（　　）
    A．99%B．99.5%C．99.9%D．无关系

    分析 根据所给的观测值，把观测值同临界值表中的临界值进行比较，看出所求的结果比哪一个临界值大，得到可信度．

    解答 解：

    P（x2≥0）0.500.400.250.150.100.050.0250.0100.0050.001
    x00.4550.7081.3232.0722.7063.8415.0246.6357.87910.828
    ∵由一个2×2列联表中的数据计算得K2的
    观测值k=7.097，
    则7.097＞6.635，
    ∴有99%的把握说这两个变量有关系，
    故选A．

    点评 本题考查独立性检验，考查判断两个变量之间有没有关系，一般题目需要自己做出观测值，再拿着观测值同临界值进行比较，得到结论，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    16．如图，在多面体EF-ABCD中，ABCD，ABEF均为直角梯形，$∠ABE=∠ABC=\frac{π}{2}$，DCEF为平行四边形，平面DCEF⊥平面ABCD．
    （Ⅰ）求证：DF⊥平面ABCD；
    （Ⅱ）若△ABD是等边三角形，且BF与平面DCEF所成角的正切值为$\frac{{\sqrt{2}}}{2}$，求二面角A-BF-C的平面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．自主招生联盟成形于2009年清华大学等五校联考，主要包括“北约”联盟，“华约”联盟，“卓越”联盟和“京派”联盟，在调查某高中学校高三学生自主招生报考的情况，得到如下结果（　　）
    ①报考“北约”联盟的考生，都没报考“华约”联盟
    ②报考“华约”联盟的考生，也报考了“京派”联盟
    ③报考“卓越”联盟的考生，都没报考“京派”联盟
    ④不报考“卓越”联盟的考生，就报考“华约”联盟
    根据上述调查结果，下述结论错误的是（　　）
    A．没有同时报考“华约”和“卓越”联盟的考生
    B．报考“华约”和“京派”联盟的考生一样多
    C．报考“北约”联盟的考生也报考了“卓越”联盟
    D．报考“京派”联盟的考生也报考了“北约”联盟

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．已知某几何体的三视图如图所示，该几何体的体积为（　　）
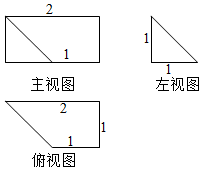
    A．$\frac{2}{3}$B．$\frac{5}{6}$C．$\frac{1}{2}$D．1

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．2015年下半年，“豆芽花”发卡突然在全国流行起来，各地随处可见头上遍插“小草”的人群，其形象如图1所示：

    对这种头上长“草”的呆萌造型，大家褒贬不一．为了了解人们是否喜欢这种造型，随机从人群中选取50人进行调查，每位被调查者都需要按照百分制对这种造型进行打分．按规定，如果被调查者的打分超过60分，那么被调查者属于喜欢这种造型的人；否则，属于不喜欢这种造型的人．将收集的分数分成[0，20]，（20，40]，（40，60]，（60，80]，（80，100]五组，并作出如下频率分布直方图（如图2）：
    （Ⅰ）为了了解被调查者喜欢这种造型是否与喜欢动画片有关，根据50位被调查者的情况制作的2×2列联表如下表，请在表格空白处填写正确数字，并说明是否有95%以上的把握认为被调查者喜欢头上长“草”的造型与自身喜欢动画片有关？
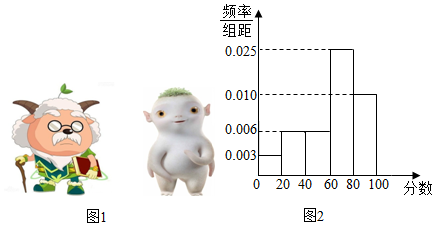
    喜欢头上长“草”的造型不喜欢头上长“草”的造型合计
    喜欢动画片30
    不喜欢动画片6
    合计
    （Ⅱ）将上述调查所得到的频率视为总体概率．现采用随机抽样方法抽取3人，记被抽取的3人中喜欢头上长“草”的造型的人数为X．若每次抽取的结果是相互独立的，求X的分布列、期望E（X）和方差D（X）．
    下面的临界值表供参考：
    P（K2≥k）0.150.100.050.0250.0100.0050.001
    k2.0722.7063.8415.0246.6357.87910.828
    （参考公式：K2=$\frac{n（ad-bc）2}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．已知函数f（x）=lnx+m（x-1）2，（m∈R）
    （Ⅰ）讨论函数f（x）极值点的个数；
    （Ⅱ）若对任意的x∈[1，+∞），f（x）≥0恒成立，求m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

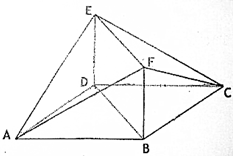    18．如图，多面ABCDEF中，DE⊥平面ABCD，底面ABCD是菱形，AB=2，∠BAD=60°，四边形BDEF是正方形．
    （1）求证：AE∥平面BCF；
    （2）求直线AF与平面ABD所成角的正弦值；
    （3）在线段EC上是否存在点P，使得AP⊥平面CEF，若存在，求出$\frac{PC}{EP}$的值；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．如图，AB为圆O的切线，A为切点，C为线段AB的中点，过C作圆O的割线CED（E在C，D之间），求证：∠CBE=∠BDE．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．若不等式$\frac{{x}^{2}-8x+20}{m{x}^{2}-mx-1}$＜0对一切x∈R都成立，则实数m的取值范围是（-4，0]．

    查看答案和解析>>

    同步练习册答案