Question

各项为正数的数列{a_n}满足＝4S_n−2a_n−1（n∈N^*），其中S_n为{a_n}前n项和．
（1）求a₁，a₂的值；
（2）求数列{a_n}的通项公式；
（3）是否存在正整数m、n，使得向量=（2a_n+2，m）与向量=（−a_n+5，3+a_n）垂直？说明理由．

Answer 1

解：（1）当n=1时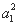，＝4S₁−2a₁−1，化简得(a₁−1)²＝0，解之得a₁=1
当n=2时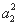，＝4S₂−2a₂−1=4（a₁+a₂）-2a₂-1
将a₁=1代入化简，得a₂²−2a₂−3＝0，解之得a₂=3或-1（舍负）
综上，a₁、a₂的值分别为a₁=1、a₂=3；
（2）由＝4S_n−2a_n−1…①，＝4S_n+1−2a_n+1−1…②
②-①，得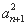−＝4a_n+1−2a_n+1+2a_n＝2(a_n+1+a_n)
移项，提公因式得（a_n+1+a_n）（a_n+1-a_n-2）=0
∵数列{a_n}的各项为正数，∴a_n+1+a_n＞0，可得a_n+1-a_n-2=0
因此，a_n+1-a_n=2，得数列{a_n}构成以1为首项，公差d=2的等差数列
∴数列{a_n}的通项公式为a_n=1+2（n-1）=2n-1；
（3）∵向量=（2a_n+2，m）与向量=（-a_n+5，3+a_n）
∴结合（2）求出的通项公式，得=（2（2n+3），m），=（-（2n+9），2n+2）
若向量⊥，则•=-2（2n+3）（2n+9）+m（2n+2）=0
化简得m=4（n+1）+16+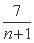
∵m、n是正整数，∴当且仅当n+1=7，即n=6时，m=45，可使⊥符合题意
综上所述，存在正整数m=45、n=6，能使向量=（2a_n+2，m）与向量=（-a_n+5，3+a_n）垂直．