
(满分13分)如图,已知△ABC是正三角形,EA、CD都垂直于平面ABC,且EA=AB=2a,DC=a,F是BE的中点,

求证: (1)FD∥平面ABC;
(1)FD∥平面ABC;
(2)AF⊥平面EDB.
(1)证明见解析;(2)证明见解析.
【解析】
试题分析:(1)取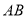 的中点
的中点 ,连接
,连接 ,利用三角形的中位线定理得出四边形
,利用三角形的中位线定理得出四边形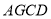 为平行四边形,再利用线面平行的判定定理进行证明;(2)利用等腰三角形的三线合一证明
为平行四边形,再利用线面平行的判定定理进行证明;(2)利用等腰三角形的三线合一证明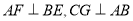 ,再利用线面垂直的判定与性质进行证明.
,再利用线面垂直的判定与性质进行证明.
解题思路: 空间中线面的平行或垂直关系的判定与证明,要注意线线关系、线面关系、面面关系的相互转化,合理结合平面几何知识进行证明.
试题解析:(1)取AB中点G,连CG,FG,由已知中F是BE的中点,结合三角形中位线的性质,可得FG平行且等于AE的一半,又由EA、CD都垂直于平面ABC,且EA=2a,DC=a,可得四边形DEGC是平行四边形,进而得到DF∥CG,由线面平行的判定定理即可得到FD∥平面ABC;
(2)由已知中EA垂直于平面ABC,则EA⊥CG,又由△ABC是正三角形,可得CG⊥AB,由线面垂直的判定定理,可得CG⊥平面EAB,进而DF⊥平面EAB,结合面面垂直的判定定理即可得到平面EAB⊥平面EDB.
证明:(1)取AB中点G,连CG,FG
四边形DEGC是平行四边形,
得到DF∥CG
DF?平面ABC,CG?平面ABC
所以FD∥平面ABC;
(2)可以证明CG⊥平面EAB,
又DF∥CG,所以DF⊥平面EAB
DF?平面EBD,所以,平面EAB⊥平面EDB
考点:1.线面平行的判定;2.线面垂直的判定与性质.


科目:高中数学 来源:2014-2015学年江苏省年高一12月月考数学试卷(解析版) 题型:填空题
已知扇形的中心角是 ,所在圆的半径为10cm,则扇形的面积为___________.
,所在圆的半径为10cm,则扇形的面积为___________.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年河南省高二上学期第四次月考理科数学试卷(解析版) 题型:选择题
抛物线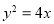 的焦点为
的焦点为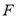 ,准线为
,准线为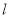 ,经过
,经过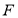 且斜率为
且斜率为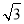 的直线与抛物线在
的直线与抛物线在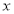 轴上方的部分相交于点
轴上方的部分相交于点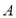 ,
,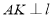 ,垂足为
,垂足为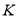 ,则
,则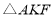 的面积是( )
的面积是( )
A.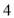 B.
B.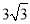 C.
C.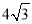 D.8
D.8
查看答案和解析>>
科目:高中数学 来源:2014-2015学年甘肃省天水市高一上学期期末考试数学试卷(解析版) 题型:选择题
设m,n是两条不同的直线,α,β,γ是三个不同的平面,给出下列四个命题:
①m⊥α,n∥α,则m⊥n;
②若α γ=m,β
γ=m,β γ=n,m∥n ,则α∥β;
γ=n,m∥n ,则α∥β;
③若α∥β,β∥γ, m⊥α,则m⊥γ;
④若α⊥γ,β⊥γ,则α∥β.
其中正确命题的序号是 ( )
A.①和③ B.②和③ C.③和④ D.①和④
查看答案和解析>>
科目:高中数学 来源:2014-2015学年甘肃省高一上学期期末考试数学试卷(解析版) 题型:填空题
一个四边形的斜二测直观图是一个底角为45°,腰和上底的长均为1的等腰梯形,那么原四边形的面积是______ 。
查看答案和解析>>
科目:高中数学 来源:2014-2015学年福建省三明市高二上学期第二次月考理科数学试卷(解析版) 题型:填空题
设S为复数集C的非空子集.若对任意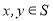 ,都有
,都有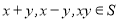 ,则称S为封闭集。下列命题:
,则称S为封闭集。下列命题:
①集合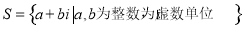 为封闭集;
为封闭集;
②封闭集一定是无限集;
③若S为封闭集,则一定有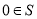 ;
;
④若S为封闭集,则满足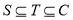 的任意集合
的任意集合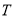 也是封闭集.
也是封闭集.
其中真命题是 (写出所有真命题的序号)
查看答案和解析>>
科目:高中数学 来源:2014-2015学年山东省烟台市高三期末考试文科数学试卷(解析版) 题型:解答题
已知数列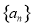 中,
中,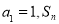 为其前
为其前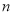 项和,且对任意
项和,且对任意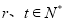 ,都有
,都有 .
.
(1)求数列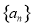 的通项公式;
的通项公式;
(2)设数列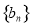 满足
满足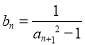 ,求数列
,求数列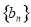 的前
的前 项和
项和 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com