
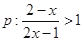 ,命题
,命题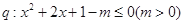 若非p是非q的必要不充分条件,那么实数m的取值范围是 。
若非p是非q的必要不充分条件,那么实数m的取值范围是 。科目:高中数学 来源:不详 题型:填空题
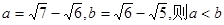 ;(2)对判断“
;(2)对判断“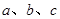 都大于零”的反设是“
都大于零”的反设是“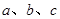 不都大于零”;(3)“
不都大于零”;(3)“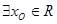 ,使得
,使得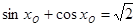 ”的否定是“对
”的否定是“对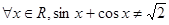 ”;(4)某产品销售量
”;(4)某产品销售量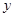 (件)与销售价格
(件)与销售价格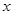 (元/件)负相关,则其回归方程
(元/件)负相关,则其回归方程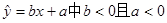 ,以上判断正确的是_________。
,以上判断正确的是_________。查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
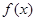 ,若
,若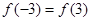 ,则函数
,则函数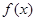 不是奇函数;
不是奇函数;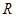 上的函数
上的函数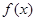 ,在区间
,在区间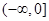 上是单调增函数,在区间
上是单调增函数,在区间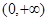 上也是单调增函数,则函数
上也是单调增函数,则函数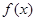 在
在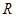 上是单调增函数;
上是单调增函数;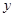 =
=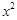 ,它的值域为
,它的值域为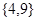 ,那么这样的函数有9个;
,那么这样的函数有9个; ,若函数
,若函数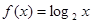 ,则
,则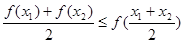
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
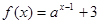
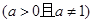 的图像一定过定点
的图像一定过定点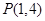 ;
;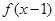 的定义域是
的定义域是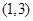 ,则函数
,则函数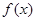 的定义域为
的定义域为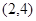 ;
;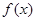 =
=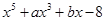 ,且
,且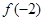 =8,则
=8,则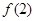 =-8;
=-8;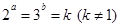 且
且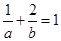 ,则实数
,则实数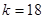 .
. 查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
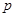 :“任意非零向量
:“任意非零向量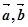 ,都有
,都有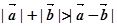 ”,则
”,则A.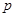 是假命题; 是假命题;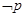 :任意非零向量 :任意非零向量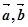 ,都有 ,都有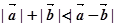 |
B.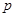 是假命题; 是假命题;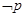 :存在非零向量 :存在非零向量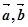 ,使 ,使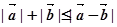 |
C.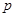 是真命题; 是真命题;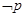 :任意非零向量 :任意非零向量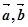 ,都有 ,都有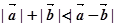 |
D.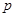 是真命题; 是真命题;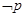 :存在非零向量 :存在非零向量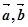 ,使 ,使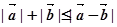 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.0 | B.1 | C.2 | D.3 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
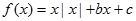 ,给出下列四个命题:
,给出下列四个命题: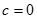 时,
时,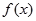 是奇函数 ②
是奇函数 ②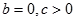 时,方程
时,方程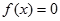 只有一个实根
只有一个实根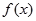 的图象关于
的图象关于 对称 ④方程
对称 ④方程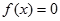 至多两个实数根
至多两个实数根| A.1 | B.2 | C.3 | D.4 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.命题“若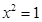 ,则 ,则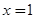 ”的否命题为:“若 ”的否命题为:“若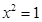 ,则 ,则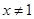 ”. ”. |
B.若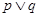 为真命题,则 为真命题,则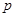 、 、 均为真命题;. 均为真命题;. |
C.命题“存在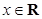 ,使得 ,使得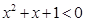 ”的否定是:“对任意 ”的否定是:“对任意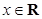 , ,均有 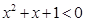 ”. ”. |
D.命题“若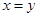 ,则 ,则 ”的逆否命题为真命题. ”的逆否命题为真命题. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com