
【题目】已知抛物线C:y2=4x和直线l:x=-1.
(1)若曲线C上存在一点Q,它到l的距离与到坐标原点O的距离相等,求Q点的坐标;
(2)过直线l上任一点P作抛物线的两条切线,切点记为A,B,求证:直线AB过定点.
【答案】(1) ![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】试题分析:(1)设Q(x,y),则(x+1)2=x2+y2,又y2=4x,解得Q![]() ;(2)设点(-1,t)的直线方程为y-t=k(x+1),联立y2=4x,则Δ=0,得k2+kt-1=0,则切点分别为A
;(2)设点(-1,t)的直线方程为y-t=k(x+1),联立y2=4x,则Δ=0,得k2+kt-1=0,则切点分别为A![]() ,B
,B![]() ,所以A,B,F三点共线,AB过点F(1,0)。
,所以A,B,F三点共线,AB过点F(1,0)。
试题解析:
(1)设Q(x,y),则(x+1)2=x2+y2,即y2=2x+1,
由![]() 解得Q
解得Q![]() .
.
(2)设过点(-1,t)的直线方程为y-t=k(x+1)(k≠0),代入y2=4x,得ky2-4y+4t+4k=0,
由Δ=0,得k2+kt-1=0,
特别地,当t=0时,k=±1,切点为A(1,2),B(1,-2),显然AB过定点F(1,0).
一般地方程k2+kt-1=0有两个根,
∴k1+k2=-t,k1k2=-1,
∴两切点分别为A![]() ,B
,B![]() ,
,
∴![]() =
=![]() ,
,![]() =
=![]() ,
,
又![]()
![]() -
-![]()
![]() =2
=2![]()
![]() =0,
=0,
∴![]() 与
与![]() 共线,又
共线,又![]() 与
与![]() 有共同的起点F,
有共同的起点F,
∴A,B,F三点共线,∴AB过点F(1,0),
综上,直线AB过定点F(1,0).


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,某大型水上乐园内有一块矩形场地![]() 米,
米, ![]() 米,以
米,以![]() 为直径的半圆
为直径的半圆![]() 和半圆
和半圆![]() (半圆在矩形
(半圆在矩形![]() 内部)为两个半圆形水上主题乐园,
内部)为两个半圆形水上主题乐园, ![]() 都建有围墙,游客只能从线段
都建有围墙,游客只能从线段![]() 处进出该主题乐园.为了进一步提高经济效益,水上乐园管理部门决定沿着
处进出该主题乐园.为了进一步提高经济效益,水上乐园管理部门决定沿着![]() 修建不锈钢护栏,沿着线段
修建不锈钢护栏,沿着线段![]() 修建该主题乐园大门并设置检票口,其中
修建该主题乐园大门并设置检票口,其中![]() 分别为
分别为![]() 上的动点,
上的动点, ![]() ,且线段
,且线段![]() 与线段
与线段![]() 在圆心
在圆心![]() 和
和![]() 连线的同侧.已知弧线部分的修建费用为
连线的同侧.已知弧线部分的修建费用为![]() 元/米,直线部门的平均修建费用为
元/米,直线部门的平均修建费用为![]() 元/米.
元/米.

(1)若![]() 米,则检票等候区域(其中阴影部分)面积为多少平方米?
米,则检票等候区域(其中阴影部分)面积为多少平方米?
(2)试确定点![]() 的位置,使得修建费用最低.
的位置,使得修建费用最低.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|x+ ![]() |+|x﹣2m|(m>0). (Ⅰ)求证:f(x)≥8恒成立;
|+|x﹣2m|(m>0). (Ⅰ)求证:f(x)≥8恒成立;
(Ⅱ)求使得不等式f(1)>10成立的实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正△ABC三个顶点都在半径为2的球面上,球心O到平面ABC的距离为1,点E是线段AB的中点,过点E作球O的截面,则截面面积的最小值是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】参与舒城中学数学选修课的同学对某公司的一种产品销量与价格进行了统计,得到如下数据和散点图.
定价x(元/千克) | 10 | 20 | 30 | 40 | 50 | 60 |
年销量y(千克) | 1150 | 643 | 424 | 262 | 165 | 86 |
z=2 ln y | 14.1 | 12.9 | 12.1 | 11.1 | 10.2 | 8.9 |

参考数据:
![]() ,
,
![]() .
.
(1)根据散点图判断y与x,z与x哪一对具有较强的线性相关性(给出判断即可,不必说明理由)?
(2)根据(1)的判断结果及数据,建立y关于x的回归方程(方程中的系数均保留两位有效数字).
(3)当定价为150元/千克时,试估计年销量.
附:对于一组数据(x1,y1),(x2,y2),(x3,y3),…,(xn,yn),其回归直线![]() x+
x+![]() 的斜率和截距的最
的斜率和截距的最
小二乘估计分别为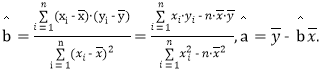
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某经销商计划销售一款新型的空气净化器,经市场调研发现以下规律:当每台净化器的利润为 x (单位:元, x 0 )时,销售量 q(x) (单位:百台)与 x 的关系满足:若 x 不超过 20 , 则 ![]() ;若 x 大于或等于180 ,则销售量为零;当 20 ≤ x ≤180 时,
;若 x 大于或等于180 ,则销售量为零;当 20 ≤ x ≤180 时,![]() ( a , b 为实常数).
( a , b 为实常数).
(Ⅰ)求函数 q(x) 的表达式;
(Ⅱ)当 x 为多少时,总利润(单位:元)取得最大值,并求出该最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com