
����Ŀ�����������ѧ��ѧѡ�ε�ͬѧ��ij��˾��һ�ֲ�Ʒ������۸������ͳ��,�õ��������ݺ�ɢ��ͼ.
����x(Ԫ/ǧ��) | 10 | 20 | 30 | 40 | 50 | 60 |
������y(ǧ��) | 1150 | 643 | 424 | 262 | 165 | 86 |
z=2 ln y | 14.1 | 12.9 | 12.1 | 11.1 | 10.2 | 8.9 |

�����:
![]() ��
��
![]() .
.
(1)����ɢ��ͼ�ж�y��x,z��x��һ�Ծ��н�ǿ�����������(�����жϼ���,����˵������)?
(2)����(1)���жϽ��������,����y����x�Ļع鷽��(�����е�ϵ����������λ��Ч����).
(3)������Ϊ150Ԫ/ǧ��ʱ,�Թ���������.
��:����һ������(x1,y1),(x2,y2),(x3,y3),��,(xn,yn),��ع�ֱ��![]() x+
x+![]() ��б�ʺͽؾ����
��б�ʺͽؾ����
С���˹��Ʒֱ�Ϊ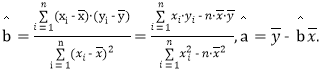
���𰸡�(1) z��x���н�ǿ�����������(2)![]() ��3������������Ϊ
��3������������Ϊ![]() =1ǧ��
=1ǧ��
��������
![]() ��ɢ��ͼ��֪z��x��Ӧ��ɢ��ͼ��������һ��ֱ�߸�������������Ը�ǿ
��ɢ��ͼ��֪z��x��Ӧ��ɢ��ͼ��������һ��ֱ�߸�������������Ը�ǿ
![]() ���ݹ�ʽ������ع鷽�̵�ϵ��������д���ع鷽��
���ݹ�ʽ������ع鷽�̵�ϵ��������д���ع鷽��
![]() ����ع鷽�����������
����ع鷽�����������
(1)��ɢ��ͼ֪, z��x���н�ǿ�����������.
(2)��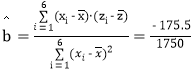 ��-0.10,
��-0.10,
��![]() ��15,��
��15,��![]() x+
x+![]() =15-0.10x.
=15-0.10x.
����z=2ln y,��y����x�Ļع鷽��Ϊ![]() .
.
(3)������Ϊ150Ԫ/ǧ��ʱ,����������Ϊ![]() =1ǧ��.
=1ǧ��.


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ʮ�Ŵ�ָ���й��ĵ綯������������չ����ͨ��������Դ���������/���ͳ����й����ڴ���ʵʩһ�����ȫ��������ҵ�ļƻ�.2019��ij��ҵ�ƻ���������Դ���������豸��ͨ���г�������ȫ����Ͷ��̶��ɱ�2500��Ԫ��ÿ����x��������������Ͷ��ɱ�![]() ��Ԫ����
��Ԫ���� .���г�����֪��ÿ�����ۼ�5��Ԫ����ȫ���������ij���������ȫ��������.
.���г�����֪��ÿ�����ۼ�5��Ԫ����ȫ���������ij���������ȫ��������.
��1�����2019�������![]() ����Ԫ�����������x���������ĺ�����ϵʽ��������=���۶�-�ɱ���
����Ԫ�����������x���������ĺ�����ϵʽ��������=���۶�-�ɱ���
��2��2019�����Ϊ���ٰ���ʱ����ҵ���������������������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����P��x��y����һ����F��1��0���ľ��������һ��ֱ��l��x=4�ľ���֮��Ϊ ![]() ��
��
��1����P��x��y���Ĺ켣C�ķ��̣�
��2����ֱ֪��l'��x=my+1���켣C��A��B���㣬����A��B�ֱ���ֱ��l�Ĵ��ߣ���������Ϊ��D��E������AE��BD����̽����m�仯ʱ��ֱ��AE��BD�Ƿ��ཻ��һ����N�������ڶ���N���������������꣬������֤��������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������C��y2��4x��ֱ��l��x����1.
(1)������C�ϴ���һ��Q������l�ľ����뵽����ԭ��O�ľ�����ȣ���Q������ꣻ
(2)��ֱ��l����һ��P�������ߵ��������ߣ��е��ΪA��B����֤��ֱ��AB������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���� ![]() ��
��
��1����m=1ʱ����֤����x��[0��+�ޣ�ʱ��f��x����0��
��2����m��1ʱ�����ۺ���f��x�����ĸ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������[0��2]����ȡ����ʵ��a��b������f��x��=x3+ax��b������[��1��1]������ֻ��һ�����ĸ����ǣ� ��
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������P��ABCD�У�PA����ABCD��AB��CD��CD��AD��AD=CD=2AB=2��E��F�ֱ�ΪPC��CD���е� 
��1����֤��ƽ��ABE��ƽ��BEF
��2����PA=a����ƽ��EBD��ƽ��ABCD���������Ǧȡ�[ ![]() ��
�� ![]() ]����a��ȡֵ��Χ��
]����a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ı���ABCD�У���BAD=120�㣬��BCD=60�㣬cosD=�� ![]() ��AD=DC=2��
��AD=DC=2�� 
������cos��DAC��AC�ij���
������BC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������f��x��= ![]() sin����x+�գ����أ�0����
sin����x+�գ����أ�0���� ![]() ��ͼ�����ֱ��x=
��ͼ�����ֱ��x= ![]() �Գƣ���ͼ��������������ߵ�ľ���Ϊ�У���
�Գƣ���ͼ��������������ߵ�ľ���Ϊ�У��� ![]() ��0�������У�����
��0������������ ![]() =�� ��
=�� ��
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com