
| A. | 等边三角形 | B. | 等腰直角三角形 | ||
| C. | 直角三角形但不是等腰三角形 | D. | 等腰三角形但不是直角三角形 |
分析 设P($\frac{{m}^{2}}{2p},m$),过点P的切线方程为:my=p(x+$\frac{{m}^{2}}{2p}$),
点Q(-$\frac{P}{2}$,0)在my=p(x+$\frac{{m}^{2}}{2p}$)上,0=(-$\frac{p}{2}$+$\frac{{m}^{2}}{2p}$)⇒m=p即可判定△PFQ的形状..
解答 解:设P($\frac{{m}^{2}}{2p},m$),过点P的切线方程为:my=p(x+$\frac{{m}^{2}}{2p}$),
点Q(-$\frac{P}{2}$,0)在my=p(x+$\frac{{m}^{2}}{2p}$)上,0=(-$\frac{p}{2}$+$\frac{{m}^{2}}{2p}$)⇒m=p
∴P($\frac{p}{2}$,p).
故PF⊥x轴,且QF=PF=p,则△PFQ一定是等腰直角三角形,
故选:B.
点评 本题考查抛物线的切线方程及抛物线的性质,属于基础题,


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{16}{625}$ | B. | $\frac{96}{625}$ | C. | $\frac{624}{625}$ | D. | $\frac{4}{625}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
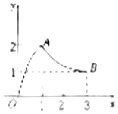 如图,函数f(x)的图象是曲线OAB,其中点O,A,B的坐标分别为(0,0),(1,2),(3,1),则$f[{\frac{1}{f(3)}}]$的值等于2.
如图,函数f(x)的图象是曲线OAB,其中点O,A,B的坐标分别为(0,0),(1,2),(3,1),则$f[{\frac{1}{f(3)}}]$的值等于2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com