
分析 (Ⅰ)由曲线y=f(x)过点P(1,-1),可得-1=ln1-m,解得m,再利用导数的几何意义可得切线的斜率,利用点斜式可得切线方程.
(Ⅱ)求出f′(x),对m分类讨论,利用导数研究函数的单调性即可得出最值.
(Ⅲ)结合(Ⅱ)的结论,证明即可.
解答 解:(Ⅰ)∵曲线y=f(x)过点P(1,-1),∴-1=ln1-m,解得m=1.
∴f(x)=lnx-x,f′(x)=$\frac{1}{x}$-1,
f′(1)=0,
∴过点P(1,-1)的切线方程为y=-1.
(Ⅱ)∵f′(x)=$\frac{1}{x}$-m=$\frac{1-mx}{x}$.
①当m≤0时,f'(x)>0,
∴f(x)在(0,+∞)为单增函数,∵在x∈[1,e]上,f(x)max=f(e)=1-me.
②当$\frac{1}{e}$<m<1时,即1<$\frac{1}{m}$<e时,x∈(0,$\frac{1}{m}$)时,f'(x)>0,f(x)为单增函数.
x∈($\frac{1}{m}$,+∞)时,f'(x)<0,f(x)为单减函数.
∴x∈[1,e]上,f(x)max=f($\frac{1}{m}$)=-lnm-1.
③当m≥1时,0<$\frac{1}{m}$≤1,f(x)在($\frac{1}{m}$,+∞)为单减函数,
∴x∈[1,e]上,f(x)max=f(1)=-m.
④当0<m≤$\frac{1}{e}$时,$\frac{1}{m}$≥e,f(x)在(0,$\frac{1}{m}$)为单增函数,
∴x∈[1,e]上,f(x)max=f(e)=1-me.
综上所述:m≤$\frac{1}{e}$时,f(x)max=f(e)=1-me.
当$\frac{1}{e}$<m<1时,f(x)max=f($\frac{1}{m}$)=-lnm-1.
当m≥1时,x∈[1,e]上,f(x)max=f(1)=-m.
(Ⅲ)由(Ⅱ)②得:m=$\frac{1}{2}$,f(x)max=f($\frac{1}{m}$)=f(2)=-ln2-1<0,
故x∈[1,e],lnx<$\frac{x}{2}$.
点评 本题考查了利用导数研究函数的单调性极值、解不等式、导数的几何意义,考查了分类讨论方法、推理能力与计算能力,属于难题.


 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案科目:高中数学 来源: 题型:选择题
| A. | {2,3,4,5} | B. | {5} | C. | {1,6} | D. | {1,2,3,4,6} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 日期 | 10月1日 | 10月2日 | 10月3日 | 10月4日 | 10月5日 |
| 价格x(元) | 9 | 9.5 | 10 | 10.5 | 11 |
| 销售量y(万件) | 11 | 10 | 8 | 6 | 5 |
| A. | 14.2元 | B. | 10.8元 | C. | 14.8元 | D. | 10.2元 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
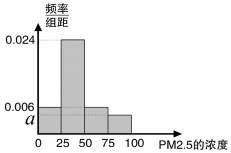 根据国家环保部新修订的《环境空气质量标准》规定:居民区PM2.5的年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米.我市环保局随机抽取了一居民区2016年20天PM2.5的24小时平均浓度(单位:微克/立方米)的监测数据,数据统计如表
根据国家环保部新修订的《环境空气质量标准》规定:居民区PM2.5的年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米.我市环保局随机抽取了一居民区2016年20天PM2.5的24小时平均浓度(单位:微克/立方米)的监测数据,数据统计如表| 组别 | PM2.5浓度 (微克/立方米) | 频数(天) | 频率 |
| 第一组 | (0,25] | 3 | 0.15 |
| 第二组 | (25,50] | 12 | 0.6 |
| 第三组 | (50,75] | 3 | 0.15 |
| 第四组 | (75,100] | 2 | 0.1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 等边三角形 | B. | 等腰直角三角形 | ||
| C. | 直角三角形但不是等腰三角形 | D. | 等腰三角形但不是直角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{3}$ | B. | $\frac{5}{4}$ | C. | $\frac{5}{3}$或$\frac{5}{4}$ | D. | $\frac{5}{3}$或$\frac{5}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
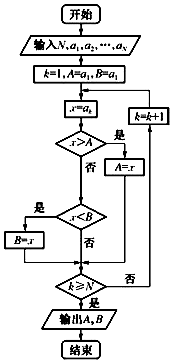 如果执行如图所示的程序框图,输入正整数N(N≥2)和实数a1,a2,…,aN,输出A,B,则( )
如果执行如图所示的程序框图,输入正整数N(N≥2)和实数a1,a2,…,aN,输出A,B,则( )| A. | A+B为a1,a2,…,aN的和 | |
| B. | A和B分别是a1,a2,…,aN中最大的数和最小的数 | |
| C. | $\frac{A+B}{2}$为a1,a2,…,aN的算术平均数 | |
| D. | A和B分别是a1,a2,…,aN中最小的数和最大的数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com