
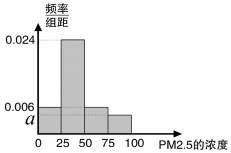
 根据国家环保部新修订的《环境空气质量标准》规定:居民区PM2.5的年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米.我市环保局随机抽取了一居民区2016年20天PM2.5的24小时平均浓度(单位:微克/立方米)的监测数据,数据统计如表
根据国家环保部新修订的《环境空气质量标准》规定:居民区PM2.5的年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米.我市环保局随机抽取了一居民区2016年20天PM2.5的24小时平均浓度(单位:微克/立方米)的监测数据,数据统计如表| 组别 | PM2.5浓度 (微克/立方米) | 频数(天) | 频率 |
| 第一组 | (0,25] | 3 | 0.15 |
| 第二组 | (25,50] | 12 | 0.6 |
| 第三组 | (50,75] | 3 | 0.15 |
| 第四组 | (75,100] | 2 | 0.1 |
分析 (1)设PM2.5的24小时平均浓度在(50,75]内的三天记为A1,A2,A3,PM2.5的24小时平均浓度在(75,100)内的两天记为B1,B2,求出基本事件总数,符合条件的基本事件总数,即可求得概率;
(2)①由第四组的频率为:0.1得:25a=0.1,解得a值;
②利用组中值×频数,可得去年该居民区PM2.5年平均浓度,进而可判断该居民区的环境是否需要改进.
解答 解:(1)设PM2.5的24小时平均浓度在(50,75]内的三天记为A1,A2,A3,
PM2.5的24小时平均浓度在(75,100)内的两天记为B1,B2.
所以5天任取2天的情况有:
A1A2,A1A3,A1B1,A1B2,A2A3,A2B1,A2B2,A3B1,A3B2共10种. …(4分)
其中符合条件的有:A1B1,A1B2,A2B1,A2B2,A3B1,A3B2共6种. …(6分)
所以所求的概率P=$\frac{6}{10}$=$\frac{3}{5}$. …(8分)
(2)①由第四组的频率为:0.1得:25a=0.1,
解得:a=0.004
②去年该居民区PM2.5年平均浓度为:12.5×0.15+37.5×0.6+62.5×0.15+87.5×0.1=42.5(微克/立方米).…(10分)
因为42.5>35,
所以去年该居民区PM2.5年平均浓度不符合环境空气质量标准,故该居民区的环境需要改进. …(12分)
点评 本题主要考查频率分布表、古典概型、统计等基础知识,考查数据处理能力、运算求解能力以及应用意识,考查必然与或然思想等.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
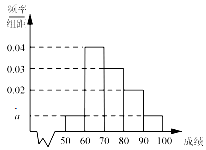 某校100名学生期中考试物理成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].
某校100名学生期中考试物理成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].查看答案和解析>>
科目:高中数学 来源: 题型:填空题
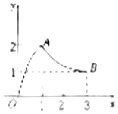 如图,函数f(x)的图象是曲线OAB,其中点O,A,B的坐标分别为(0,0),(1,2),(3,1),则$f[{\frac{1}{f(3)}}]$的值等于2.
如图,函数f(x)的图象是曲线OAB,其中点O,A,B的坐标分别为(0,0),(1,2),(3,1),则$f[{\frac{1}{f(3)}}]$的值等于2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
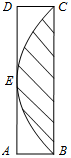 如图所示矩形ABCD边长AB=1,AD=4,抛物线顶点为边AD的中点E,且B,C两点在抛物线上,则从矩形内任取一点落在抛物线与边BC围成的封闭区域(包含边界上的点)内的概率是$\frac{2}{3}$.
如图所示矩形ABCD边长AB=1,AD=4,抛物线顶点为边AD的中点E,且B,C两点在抛物线上,则从矩形内任取一点落在抛物线与边BC围成的封闭区域(包含边界上的点)内的概率是$\frac{2}{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com