
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 相关指数R2的值判断的拟合效果,R2越大,模型的拟合效果越好,即可判断①;
两个随机变量的线性相关性越强,相关系数的绝对值越接近1,即可判断②;
由方差的性质,可得若数据x1,x2,x3,…,xn的方差为t,
则ax1,ax2,ax3,…,axn的方差为a2t2,即可判断③;
对分类变量x与y的随机变量k2的观测值k来说,k越小,判断“x与y有关系”的把握程度越小,
即可判断④.
解答 解:①在回归分析中,可用相关指数R2的值判断的拟合效果,R2越大,模型的拟合效果越好,
故①正确;
②两个随机变量的线性相关性越强,相关系数的绝对值越接近1,故②正确;
③若数据x1,x2,x3,…,xn的方差为1,则2x1,2x2,2x3,…,2xn的方差为4,故③错误;
④对分类变量x与y的随机变量k2的观测值k来说,k越小,判断“x与y有关系”的把握程度越小,
故④错误.
其中真命题的个数为2.
故选:B.
点评 本题考查命题的真假判断,考查线性回归分析和随机变量的相关性、方差的特点,考查判断能力,属于基础题.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案科目:高中数学 来源: 题型:选择题
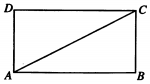 如图,在矩形ABCD中,$AB=\sqrt{3},BC=1$,将△ACD沿折起,使得D折起的位置为D1,且D1在平面ABC的射影恰好落在AB上,则直线D1C与平面ABC所成角的正弦值为( )
如图,在矩形ABCD中,$AB=\sqrt{3},BC=1$,将△ACD沿折起,使得D折起的位置为D1,且D1在平面ABC的射影恰好落在AB上,则直线D1C与平面ABC所成角的正弦值为( )| A. | $\frac{1}{3}$ | B. | $\frac{{\sqrt{2}}}{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{3}}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 0 | 1 | 2 | 3 |
| y | -1 | 1 | m | 6 |
| A. | 4 | B. | $\frac{9}{2}$ | C. | 5.5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 300 | B. | 216 | C. | 180 | D. | 162 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com