已知函数f(x)=x3+ax+b的图象是曲线C,曲线C在点(1,3)处的切线与直线y=2x+3平行.
(1)求函数f(x)的解析式;
(2)求函数f(x)的递增区间;
(3)求函数F(x)=f(x)-2x-3在区间[0,2]上的最大值和最小值.
【答案】
分析:(1)利用f(x)的导函数及切点横坐标,求出a的值;再利用切点求出b的值.最后代入即可得f(x)的解析式.
(2)通过在函数的单调递增区间,函数f(x)的导函数大于零,求出x的取值范围.
(3)通过函数F(x)的导函数F'(x)=0,求出函数的极值.列出x,F'(x),F(x)关系表,通过观察可知F(x)在区间[0,2]最大和最小值.
解答:解:(1)根据题意:.∵f'(x)=3x
2+a
∴f'(1)=3+a=2得a=-1
由f(1)=3得1+a+b=3,∴b=3
∴f(x)=x
3-x+3.
(2)由f(x)=x
3-x+3得f'(x)=3x
2-1,
令f'(x)=3x
2-1>0,解得
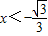
或
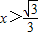
.
∴函数f(x)的递增区间为
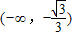
,
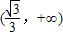
.
(3)F(x)=x
3-3x,F'(x)=3x
2-3
令F'(x)=3x
2-3=0,得x
1=-1,x
2=1.
列出x,F'(x),F(x)关系如下:
| x | | (0,1) | 1 | (1,2) | 2 |
| F'(x) | | - | | + | |
| F(x) | | 递减 | 极小值-2 | 递增 | 2 |
∴当x∈[0,2]时,F(x)的最大值为2,最小值为-2
点评:本题主要考查了用待定系数法求函数的解析式.解此类题常用到导函数与函数的关系来解决问题.

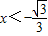 或
或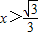 .
.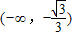 ,
,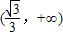 .
.

 名校课堂系列答案
名校课堂系列答案 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<