
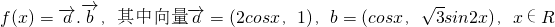
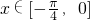 ,求函数f(x)的值域.
,求函数f(x)的值域.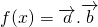 =2cos2x+
=2cos2x+ sin2x
sin2x sin2x+cos2x+1=2sin(2x+
sin2x+cos2x+1=2sin(2x+ )+1
)+1 +2kπ≤2x+
+2kπ≤2x+ ≤
≤ +2kπ,得kπ+
+2kπ,得kπ+ ≤x≤kπ+
≤x≤kπ+ ,k∈Z,
,k∈Z, ,kπ+
,kπ+ ],k∈Z,
],k∈Z,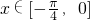 时,2x+
时,2x+ ∈[-
∈[- ,
, ].
]. )∈[-
)∈[- ,
, ],得y=2sin(2x+
],得y=2sin(2x+ )+1∈[-
)+1∈[- +1,2]
+1,2] 的值域是[-
的值域是[- +1,2].
+1,2]. )+1.再根据正弦函数的单调区间的公式,解不等式可得函数f(x)的单调减区间;
)+1.再根据正弦函数的单调区间的公式,解不等式可得函数f(x)的单调减区间; 易得2x+
易得2x+ ∈[-
∈[- ,
, ].结合正弦函数的图象与性质,得2sin(2x+
].结合正弦函数的图象与性质,得2sin(2x+ )∈[-
)∈[- ,
, ],由此不难得到函数f(x)在区间
],由此不难得到函数f(x)在区间 的值域.
的值域.

 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:
 设函数f(x)=
设函数f(x)=
|
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2009•成都模拟)设函数f(x)=
(2009•成都模拟)设函数f(x)=
|
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年岳阳一中二模文)(12分)
设函数![]()
(1)求函数f(x)的单调区间,并求函数f(x)的极大值和极小值;
(2)当x∈[a+1, a+2]时,不等![]() ,求a的取值范围.
,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省泰州市姜堰市蒋垛中学高三数学综合练习2(文科)(解析版) 题型:解答题

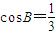 ,
,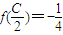 ,且C为锐角,求sinA的值.
,且C为锐角,求sinA的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com