
分析 (1)把$sinA+cosA=\frac{1}{5}$两边平方,得1+2sinA•cosA=$\frac{1}{25}$,从而sinA•cosA=-$\frac{12}{25}$.进而A为钝角,由此得到△ABC是钝角三角形.
(2)由sinA•cosA=-$\frac{12}{25}$,sin2A+cos2A=1,求出sinA=$\frac{4}{5}$,cosA=-$\frac{3}{5}$,由此能求出tanA.
解答 解:(1)在△ABC中,∵$sinA+cosA=\frac{1}{5}$,
∴两边平方可得1+2sinA•cosA=$\frac{1}{25}$,
∴sinA•cosA=-$\frac{12}{25}$.
∵0<A<π,∴A为钝角,∴△ABC是钝角三角形.
(2)∵sinA•cosA=-$\frac{12}{25}$,
又sin2A+cos2A=1,
∴sinA=$\frac{4}{5}$,cosA=-$\frac{3}{5}$,
∴tanA=$\frac{sinA}{cosA}$=-$\frac{4}{3}$.
点评 本题考查三角形形状的判断,考查三角形的角的正切值的求法,考查同角三角函数关系式、三角形性质等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | 0.3413 | B. | 0.4772 | C. | 0.8185 | D. | 0.1359 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
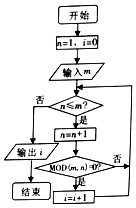 已知MOD函数是一个求余函数,MOD(m,n)表示m除以n的余数,例如MOD(8,3)=2,如图是某个算法的程序框图,若输入m的值为6,则输出i的值为( )
已知MOD函数是一个求余函数,MOD(m,n)表示m除以n的余数,例如MOD(8,3)=2,如图是某个算法的程序框图,若输入m的值为6,则输出i的值为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com