
分析 利用奇偶性将不等式进行转化,再利用单调性去掉不等式中的符号“f”,转化具体不等式,借助一次函数的性质可得x的不等式组,解出可得答案.
解答 解:由题意,奇函数f(x)在R上为增函数,
所以f(mx-2)+f(x)<0可化为:f(mx-2)<-f(x)=f(-x),
由f(x)递增知:mx-2<-x,即mx+x-2<0,
则对任意的m∈[-2,2],f(mx-2)+f(x)<0恒成立,
等价于对任意的m∈[-2,2],mx+x-2<0恒成立,
所以$\left\{\begin{array}{l}{-2x+x-2<0}\\{2x+x-2<0}\end{array}\right.$,解得-2<x<$\frac{2}{3}$,
即x的取值范围是(-2,$\frac{2}{3}$),
故答案为:(-2,$\frac{2}{3}$).
点评 本题考查恒成立问题,函数的奇偶性与单调性的综合应用,考查转化思想,以及学生灵活运用知识解决问题的能力.


 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
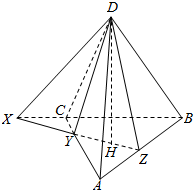 过正四面体ABCD的高DH作一平面,与正四面体的三个侧面相交得到三条直线DX,DY,DZ,这三条直线与正四面体的底面所成角分别为$\alpha$,$\beta$,$\gamma$.求证:tan2α+tan2β+tan2γ=12.
过正四面体ABCD的高DH作一平面,与正四面体的三个侧面相交得到三条直线DX,DY,DZ,这三条直线与正四面体的底面所成角分别为$\alpha$,$\beta$,$\gamma$.求证:tan2α+tan2β+tan2γ=12.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com