
分析 利用条件,求f(0)+f(1),f(-1)+f(2),f(-2)+f(3),归纳猜想一般性结论,利用指数的性质给出证明.
解答 解:f(0)+f(1)=$\frac{1}{2}$,
同理可得:f(-1)+f(2)=$\frac{1}{2}$,f(-2)+f(3)=$\frac{1}{2}$.
一般性结论:$f(x)+f(1-x)=\frac{1}{2}$或写成“若x1+x2=1,则f(x1)+f(x2)=$\frac{1}{2}$.”
证明:$f(x)+f(1-x)=\frac{1}{{{4^x}+2}}+\frac{1}{{{4^{1-x}}+2}}=\frac{1}{{{4^x}+2}}+\frac{4^x}{{{4^x}({4^{1-x}}+2)}}$=$\frac{1}{{{4^x}+2}}+\frac{4^x}{{{4^{\;}}+2×{4^x}}}=\frac{1}{{{4^x}+2}}+\frac{4^x}{{2(2+{4^x})}}$=$\frac{{2+{4^x}}}{{2(2+{4^x})}}=\frac{1}{2}$,
点评 本题考查归纳推理,考查学生分析解决问题的能力,正确归纳猜想是关键.


 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:高中数学 来源: 题型:解答题
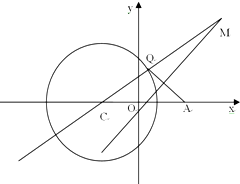 如图,已知圆$C:{(x+\sqrt{3})^2}+{y^2}=8,A(\sqrt{3},0)$,Q是圆上一动点,AQ的垂直平分线交直线CQ于点M,设点M的轨迹为E.
如图,已知圆$C:{(x+\sqrt{3})^2}+{y^2}=8,A(\sqrt{3},0)$,Q是圆上一动点,AQ的垂直平分线交直线CQ于点M,设点M的轨迹为E.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
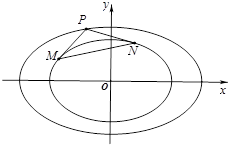 已知椭圆${C_1}:\frac{x^2}{2}+{y^2}=1$
已知椭圆${C_1}:\frac{x^2}{2}+{y^2}=1$查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2)∪(0,2) | B. | (-∞,-2)∪(2,+∞) | C. | (-2,0)∪(2,+∞) | D. | (-2,0)∪(0,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
职务 性别 | 担任学生干部 | 未担任学生干部 | 总计 |
| 男 | 10 | 16 | |
| 女 | 6 | 14 | |
| 总计 | 30 |
| P(K2≥k0) | 0.40 | 0.25 | 0.10 | 0.010 |
| k0 | 0.708 | 1.323 | 2.706 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com