
分析 由数列的前n项和求出数列{an}的通项公式,代入bn=3${\;}^{{a}_{n}}$+(-1)n-1an,然后利用数列的分组求和及等比数列的前n项和得答案.
解答 解:由Sn=$\frac{1}{2}$n(n+1),得${a}_{1}={S}_{1}=\frac{1}{2}×1×2=1$,
当n≥2时,an=Sn-Sn-1=$\frac{1}{2}n(n+1)-\frac{1}{2}(n-1)n$=n,
当n=1时上式成立,
∴an=n,
则bn=3${\;}^{{a}_{n}}$+(-1)n-1an=3n+(-1)n-1n,
∴数列{bn}的前2n+1项和为(31+32+…+32n+1)+[1-2+3-4+…+(2n-1)-2n+(2n+1)]
=$\frac{3(1-{3}^{2n+1})}{1-3}+n+1$=$\frac{1}{2}•{3}^{2n+2}+n-\frac{1}{2}$.
故答案为:$\frac{1}{2}•{3}^{2n+2}+n-\frac{1}{2}$.
点评 本题考查了等差关系的确定,考查了数列的分组求和及等比数列的前n项和,是中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
| 广告费用x(单位:万元) | 2 | 3 | 4 | 5 |
| 利润y(单位:万元) | 26 | ● | 49 | 54 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
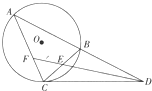 如图所示,已知A、B、C三点都在⊙O上,CD是⊙O的切线,直线AB与CD交于点D.
如图所示,已知A、B、C三点都在⊙O上,CD是⊙O的切线,直线AB与CD交于点D.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,$\frac{4}{3}$) | B. | ($\frac{4}{3}$,$\sqrt{2}$) | C. | ($\sqrt{2}$,$\sqrt{3}$) | D. | ($\sqrt{3}$,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com