
【题目】如图,AB是圆O的直径,PA⊥圆O所在的平面,C是圆O上的点. 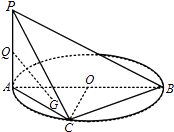
(1)求证:BC⊥平面PAC;
(2)若Q为PA的中点,G为△AOC的重心,求证:QG∥平面PBC.
【答案】
(1)证明:AB是圆O的直径,PA⊥圆所在的平面,可得PA⊥BC,
C是圆O上的点,由直径对的圆周角等于90°,可得BC⊥AC.
再由AC∩PA=A,利用直线和平面垂直的判定定理可得BC⊥平面PAC
(2)解:若Q为PA的中点,G为△AOC的重心,连接OG并延长交AC于点M,
连接QM,则由重心的性质可得M为AC的中点.
故OM是△ABC的中位线,QM是△PAC的中位线,故有OM∥BC,QM∥PC.
而OM和QM是平面OQM内的两条相交直线,AC和BC是平面PBC内的两条相交直线,故平面OQM∥平面PBC.
又QG平面OQM,∴QG∥平面PBC
【解析】(1)由PA⊥圆所在的平面,可得PA⊥BC,由直径对的圆周角等于90°,可得BC⊥AC,根据直线和平面垂直的判定定理可得结论.(2)连接OG并延长交AC于点M,则由重心的性质可得M为AC的中点.利用三角形的中位线性质,证明OM∥BC,QM∥PC,可得平面OQM∥平面PBC,从而证明QG∥平面PBC
【考点精析】通过灵活运用直线与平面平行的判定和直线与平面垂直的判定,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想即可以解答此题.


 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:
【题目】北京时间3月15日下午,谷歌围棋人工智能![]() 与韩国棋手李世石进行最后一轮较量,
与韩国棋手李世石进行最后一轮较量,![]() 获得本场比赛胜利,最终人机大战总比分定格在
获得本场比赛胜利,最终人机大战总比分定格在![]() .人机大战也引发全民对围棋的关注,某学校社团为调查学生学习围棋的情况,随机抽取了100名学生进行调查.根据调查结果绘制的学生日均学习围棋时间的频率分布直方图(如图所示),将日均学习围棋时间不低于40分钟的学生称为“围棋迷”.
.人机大战也引发全民对围棋的关注,某学校社团为调查学生学习围棋的情况,随机抽取了100名学生进行调查.根据调查结果绘制的学生日均学习围棋时间的频率分布直方图(如图所示),将日均学习围棋时间不低于40分钟的学生称为“围棋迷”.
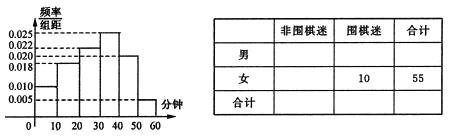
(1)根据已知条件完成如图列联表,并据此资料判断你是否有![]() 的把握认为“围棋迷”与性别有关?
的把握认为“围棋迷”与性别有关?
(2)将上述调查所得到的频率视为概率.现在从该地区大量学生中,采用随机抽样方法每次抽取1名学生,抽取3次,记所抽取的3名学生中的“围棋迷”人数为![]() .若每次抽取的结果是相互独立的,求
.若每次抽取的结果是相互独立的,求![]() 的分布列,期望
的分布列,期望![]() 和方差
和方差![]() .
.
附:![]() ,其中
,其中![]() .
.
| 0.05 | 0.010 |
| 3.74 | 6.63 |
查看答案和解析>>
科目:高中数学 来源: 题型:
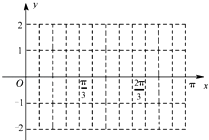
【题目】设函数f(x)=2sin(2x+φ)(0<φ<π),y=f(x)图象的一个对称中心是 ![]() .
. 
(1)求φ;
(2)在给定的平面直角坐标系中作出该函数在x∈[0,π]的图象;
(3)求函数f(x)≥1(x∈R)的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱柱ABC﹣A1B1C1的侧棱垂直于底面,且其6个顶点都在球O的球面上,若AB=3,AC=4,AB⊥AC,AA1=12,则球O的半径为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为研究患肺癌与是否吸烟有关,做了一次相关调查,其中部分数据丢失,但可以确定的是不吸烟人数与吸烟人数相同,吸烟患肺癌人数占吸烟总人数的![]() ;不吸烟的人数中,患肺癌与不患肺癌的比为
;不吸烟的人数中,患肺癌与不患肺癌的比为![]() .
.
(1)若吸烟不患肺癌的有![]() 人,现从患肺癌的人中用分层抽样的方法抽取
人,现从患肺癌的人中用分层抽样的方法抽取![]() 人,再从这
人,再从这![]() 人中随机抽取
人中随机抽取![]() 人进行调查,求这两人都是吸烟患肺癌的概率;
人进行调查,求这两人都是吸烟患肺癌的概率;
(2)若研究得到在犯错误概率不超过![]() 的前提下,认为患肺癌与吸烟有关,则吸烟的人数至少有多少?
的前提下,认为患肺癌与吸烟有关,则吸烟的人数至少有多少?
附: 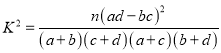 ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将参加数学竞赛的1000名学生编号如下:0001,0002,0003,…,1000,按系统抽样的方法从中抽取一个容量为50的样本,如果在第一组抽得的编号是0015,则在第21组抽得的编号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一家面包房根据以往某种面包的销售记录,绘制了日销售量的频率分布直方图,如图所示.将日销售量落入各组的频率视为概率. 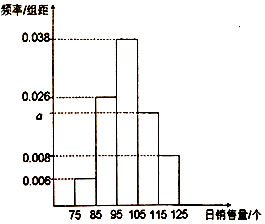
(1)求a的值并估计在一个月(按30天算)内日销售量不低于105个的天数;
(2)利用频率分布直方图估计每天销售量的平均值及方差(同一组中的数据用该组区间的中点值作代表).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的一个焦点与上、下顶点构成直角三角形,以椭圆
的一个焦点与上、下顶点构成直角三角形,以椭圆![]() 的长轴长为直径的圆与直线
的长轴长为直径的圆与直线![]() 相切.
相切.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设过椭圆右焦点且不平行于![]() 轴的动直线与椭圆
轴的动直线与椭圆![]() 相交于
相交于![]() 两点,探究在
两点,探究在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() 为定值?若存在,试求出定值和点
为定值?若存在,试求出定值和点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com