
分析 利用分段函数的表达式,直接代入进行求解即可,利用函数与方程之间的关系,转化为两个函数的交点个数问题,利用数形结合进行求解即可.
解答 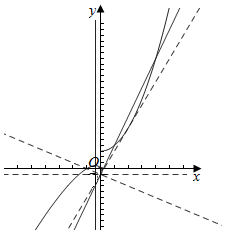 解:由分段函数的表达式得f(-$\frac{1}{2}$)=-$\frac{1}{2}$•log2$\frac{1}{2}$=$\frac{1}{2}$,
解:由分段函数的表达式得f(-$\frac{1}{2}$)=-$\frac{1}{2}$•log2$\frac{1}{2}$=$\frac{1}{2}$,
则f($\frac{1}{2}$)=($\frac{1}{2}$)2+3=$\frac{13}{4}$,
若f(x)=ax-1有三个零点,
则f(x)与y=ax-1有三个交点,
当x<0时,f(x)=xlog2(-x),
则f′(x)=log2(-x)+x$•\frac{1}{-xln2}$•(-1)
=log2(-x)+$\frac{1}{ln2}$=log2(-x)+log2e=log2(-ex),
由f′(x)>0得-ex>1,即x<-$\frac{1}{e}$,此时函数单调递增,
由f′(x)<0得-ex<1,即-$\frac{1}{e}$<x<0,此时函数单调递增,
作出函数f(x)的图象如图,
若a≤0,则f(x)与直线y=ax-1只有一个交点,不满足条件.
若a>0,当x<0时,直线y=ax-1与f(x)=xlog2(-x)一定有一个交点,
当x≥0时,当直线和f(x)=x2+3相切时,
此时也有一个交点,此时两个函数有2个交点,
由x2+3=ax-1,得x2-ax+4=0,则判别式△=a2-16=0,
得a>4或a<-4(舍),
当直线和f(x)=x2+3相交时,即a>4,此时有2个交点,
加上当x<0时的一个交点,两个函数有3个交点,
此时满足条件,
综上a>4.
故答案为:$\frac{13}{4}$,a>4.
点评 本题主要考查函数零点个数的判断以及分段函数的求值问题,利用函数与方程的关系转化为两个函数的交点问题,利用数形结合是解决本题的关键.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案科目:高中数学 来源: 题型:解答题
 如图,⊙O的圆心O在Rt△ABC的直角边BC上,AB、AC都是⊙O的切线,M是AB与⊙O相切的切点,N是⊙O与BC的交点.
如图,⊙O的圆心O在Rt△ABC的直角边BC上,AB、AC都是⊙O的切线,M是AB与⊙O相切的切点,N是⊙O与BC的交点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,2] | B. | (-∞,2) | C. | [2,+∞) | D. | [-2,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x<1} | B. | {x|x<-1} | C. | {x|-1<x<1} | D. | {x|x<-1或x>1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
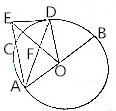 已知AB过⊙O的圆心,E为圆外的一点,ED为⊙O的一条切线,且D为切点,EA为⊙O的一条割线,且交⊙O于C,sin∠AED=1
已知AB过⊙O的圆心,E为圆外的一点,ED为⊙O的一条切线,且D为切点,EA为⊙O的一条割线,且交⊙O于C,sin∠AED=1查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
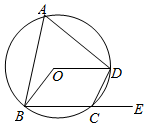
| A. | 120° | B. | 136° | C. | 144° | D. | 150° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com