
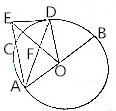
 已知AB过⊙O的圆心,E为圆外的一点,ED为⊙O的一条切线,且D为切点,EA为⊙O的一条割线,且交⊙O于C,sin∠AED=1
已知AB过⊙O的圆心,E为圆外的一点,ED为⊙O的一条切线,且D为切点,EA为⊙O的一条割线,且交⊙O于C,sin∠AED=1分析 (1)利用圆的切线的性质,即可证明AC∥OD;
(2)不妨设AC=3,AB=5,连接BC,则BC⊥AC,BC∥ED,求出ED,即可证明:AF=$\frac{8}{5}$FD.
解答 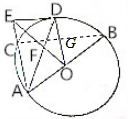 证明:(1)∵ED为⊙O的一条切线,且D为切点,
证明:(1)∵ED为⊙O的一条切线,且D为切点,
∴ED⊥OD,
∵sin∠AED=1,
∴ED⊥AE,
∴AC∥OD;
(2)不妨设AC=3,AB=5,连接BC,则BC⊥AC,BC∥ED,
∴四边形ECGD为矩形,CG=ED=2,
由切割线定理可得,ED2=EC•EA,
∴22=ED•(ED+3),
∴ED=1,
∴AE=4,
∵AC∥OD,
∴$\frac{AF}{FD}$=$\frac{AE}{OD}$=$\frac{8}{5}$,
∴AF=$\frac{8}{5}$FD.
点评 本题考查圆的切线的性质,考查切割线定理,考查学生分析解决问题的能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题

| A. | 9$\sqrt{3}$ | B. | 9$\sqrt{2}$+$\frac{9\sqrt{3}}{4}$ | C. | 12$\sqrt{2}$ | D. | 12$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x>0} | B. | {x|x<0} | C. | {x|x<-1或0<x<1} | D. | {x|x<-1或x>1} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)在R上单调递增 | B. | f(x)在R上是常数 | C. | f(x)在R上不单调 | D. | f(x)在R上单调递减 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 归纳推理 | B. | 合情推理 | C. | 演绎推理 | D. | 类比推理 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com