
分析 (1)根据f(x)为奇函数便可得出$lg\frac{1-ax}{1-x}=-lg\frac{1+ax}{1+x}$,这样便可得出1-a2x2=1-x2,从而有a2=1,再根据a≠1即可得出a的值;
(2)求出a便得出$f(x)=lg\frac{1-x}{1+x}$,从而可求出该函数的定义域,进而求出b的取值范围;
(3)由f(x)>0即可得出$lg\frac{1-x}{1+x}>lg1$,这样便可建立关于x的不等式,解不等式即可得出原不等式的解集.
解答 解:(1)f(x)为奇函数;
∴f(-x)=-f(x),即$lg\frac{1-ax}{1-x}=-lg\frac{1+ax}{1+x}$;?
即$\frac{1-ax}{1-x}=\frac{1+x}{1+ax}$,整理得:1-a2x2=1-x2;
∴a=±1;
又a≠1,故a=-1;
(2)f(x)=lg$\frac{1-x}{1+x}$的定义域是(-1,1);
∴0<b≤1;
∴b的取值范围为(0,1];
(3)f(x)=$lg\frac{1-x}{1+x}>0=lg1$;
∴$\frac{1-x}{1+x}>1$;
解得-1<x<0;
∴原不等式的解集为(-1,0).
点评 考查奇函数的定义,多项式相等的充要条件,对数的真数满足大于0,以及对数函数的单调性,分式不等式的解法.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:高中数学 来源: 题型:解答题
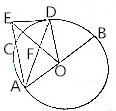 已知AB过⊙O的圆心,E为圆外的一点,ED为⊙O的一条切线,且D为切点,EA为⊙O的一条割线,且交⊙O于C,sin∠AED=1
已知AB过⊙O的圆心,E为圆外的一点,ED为⊙O的一条切线,且D为切点,EA为⊙O的一条割线,且交⊙O于C,sin∠AED=1查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
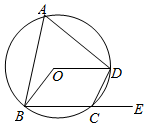
| A. | 120° | B. | 136° | C. | 144° | D. | 150° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
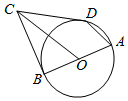 如图所示,AB是圆O的直径,BC与圆O相切于B,∠ADC+∠DCO=180°
如图所示,AB是圆O的直径,BC与圆O相切于B,∠ADC+∠DCO=180°查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com