
分析 (Ⅰ)设取球的次数为ξ,最多取两次就结束的概率P1=P(ξ=1)+P(ξ=2),由此能求出结果.
(Ⅱ)由题意可知,可以如下取球:红白白,白红白,白白红,白白蓝,由此能求出恰好取到2个白球的概率.
(Ⅲ)随机变量X的取值为1,2,3,分别求出相应的概率,由此能求出随机变量X的分布列和数学期望.
解答 (本小题满分13分)
解:(Ⅰ)设取球的次数为ξ,
则P(ξ=1)=$\frac{{C}_{3}^{1}}{{C}_{10}^{1}}$=$\frac{3}{10}$,P(ξ=2)=$\frac{{C}_{7}^{1}}{{C}_{10}^{1}}×\frac{{C}_{3}^{1}}{{C}_{10}^{1}}$=$\frac{21}{100}$,
所以最多取两次就结束的概率P1=P(ξ=1)+P(ξ=2)=$\frac{51}{100}$.…(4分)
(Ⅱ)由题意可知,可以如下取球:红白白,白红白,白白红,白白蓝,
所以恰好取到2个白球的概率:
P2=$\frac{4}{10}×\frac{3}{10}×\frac{3}{10}$×3+$\frac{3}{10}×\frac{3}{10}×\frac{3}{10}$=$\frac{135}{1000}$=$\frac{27}{200}$.…(8分)
(Ⅲ)随机变量X的取值为1,2,3 …(9分)
P(X=1)=$\frac{3}{10}$,
P(X=2)=$\frac{7}{10}×\frac{3}{10}$=$\frac{21}{100}$,
P(X=3)=$\frac{7}{10}×\frac{7}{10}×(\frac{3}{10}+\frac{7}{10})$=$\frac{49}{100}$,…(12分)
随机变量X的分布列为:
| X | 1 | 2 | 3 |
| P | $\frac{3}{10}$ | $\frac{21}{100}$ | $\frac{49}{100}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列的求法,是中档题,解题时要认真审题,注意相互独立事件概率乘法公式的合理运用.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({-\frac{π}{6},0})∪({0,\frac{π}{6}})$ | B. | $({-\frac{π}{6},0})∪({\frac{π}{6},π})$ | C. | $({-\frac{π}{6},0})∪({\frac{π}{6},\frac{π}{2}})$ | D. | $({-π,-\frac{π}{6}})∪({0,\frac{π}{6}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
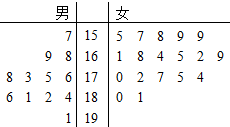 某小学对五年级的学生进行体质测试,已知五年一班共有学生30人,测试立定跳远的成绩用茎叶图表示如图(单位:cm):
某小学对五年级的学生进行体质测试,已知五年一班共有学生30人,测试立定跳远的成绩用茎叶图表示如图(单位:cm):查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知椭圆$\frac{x^2}{9}+{y^2}=1$,过A(0,1)作互相垂直的两直线AB,AC与椭圆交于B,C两点.
已知椭圆$\frac{x^2}{9}+{y^2}=1$,过A(0,1)作互相垂直的两直线AB,AC与椭圆交于B,C两点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com