
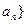 中,
中,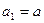 (
(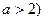 且
且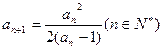
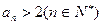 ;(2)求证
;(2)求证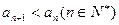 ;
;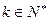 ,使得
,使得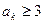 ,求证:
,求证: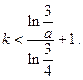
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源:不详 题型:解答题
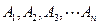 为集合
为集合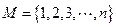 的
的 个不同的子集,对于任意不大于
个不同的子集,对于任意不大于 的正整数
的正整数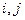 满足下列条件:
满足下列条件: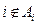 ,且每一个
,且每一个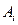 至
至 少含有三个元素;
少含有三个元素;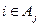 的充要条件是
的充要条件是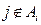 (其中
(其中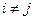 )。
)。 行
行 列的数表(即
列的数表(即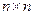 数表),规定第
数表),规定第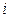 行第
行第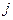 列数为:
列数为: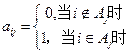 。
。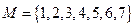 ,请完成下面
,请完成下面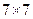 数表(填符合题意的一种即可);
数表(填符合题意的一种即可);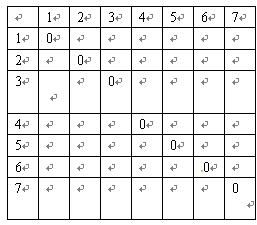
 的代数式表示
的代数式表示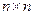 数表
数表 中1的个数
中1的个数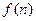 ,并证明
,并证明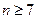 ;
;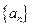 前
前 项和为
项和为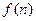 ,数列
,数列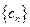 的通项公式为:
的通项公式为: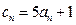 ,证明不等式:
,证明不等式: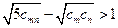 对任何正整数
对任何正整数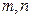 都成立。
都成立。查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
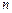 个图形包含
个图形包含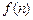 个“福娃迎迎”,
个“福娃迎迎”, ;
; ____________.(答案用数字或
____________.(答案用数字或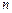 的解析式表示)
的解析式表示)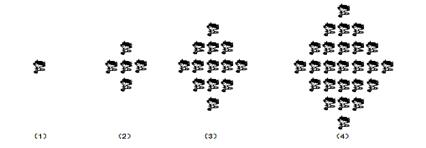
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com