
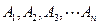 为集合
为集合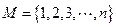 的
的 个不同的子集,对于任意不大于
个不同的子集,对于任意不大于 的正整数
的正整数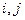 满足下列条件:
满足下列条件: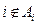 ,且每一个
,且每一个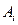 至
至 少含有三个元素;
少含有三个元素;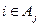 的充要条件是
的充要条件是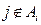 (其中
(其中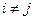 )。
)。 行
行 列的数表(即
列的数表(即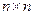 数表),规定第
数表),规定第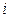 行第
行第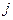 列数为:
列数为: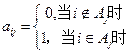 。
。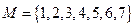 ,请完成下面
,请完成下面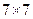 数表(填符合题意的一种即可);
数表(填符合题意的一种即可);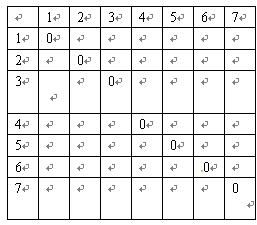
 的代数式表示
的代数式表示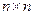 数表
数表 中1的个数
中1的个数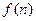 ,并证明
,并证明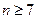 ;
;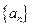 前
前 项和为
项和为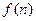 ,数列
,数列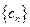 的通项公式为:
的通项公式为: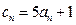 ,证明不等式:
,证明不等式: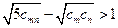 对任何正整数
对任何正整数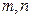 都成立。
都成立。 ,证明见解析。
,证明见解析。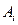 中至少含有三个元素,作出的数表每一列至少有三个1。
中至少含有三个元素,作出的数表每一列至少有三个1。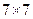 数表如下:
数表如下:| | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 2 | 1 | 0 | 0 | 1 | 0 | 0 | 1 |
 3 3 | 1 | 1 | 0 | 0 | 0 | 1 | 0 |
| 4 | 1 | 0 | 1 | 0 | 1 | 0 | 0 |
| 5 | 0 | 1 | 1 | 0 | 0 | 0 | 1 |
| 6 | 0 | 1 | 0 | 1 | 1 | 0 | 0 |
| 7 | 0 | 0 | 1 | 1 | 0 | 1 | 0 |
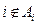 表明的一条对角线上数字都是0,题设条件②表明除对角线以外,
表明的一条对角线上数字都是0,题设条件②表明除对角线以外,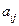 与
与 恰好一个为1,而另一个为0,即数表中除该对角线以外,0与1各占一半,故数表中共有
恰好一个为1,而另一个为0,即数表中除该对角线以外,0与1各占一半,故数表中共有 个1。另一方面,根据题设条件①每一个
个1。另一方面,根据题设条件①每一个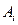 至少含有三个元素得:作出的
至少含有三个元素得:作出的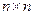 数表的每一列至少有3个1,所以整个
数表的每一列至少有3个1,所以整个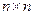 数表(共有
数表(共有 列)至少有
列)至少有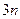 个1,因此列出不等式:
个1,因此列出不等式: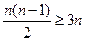 ,解得
,解得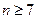 。
。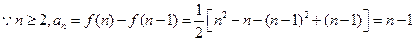
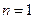 也成立,故
也成立,故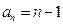
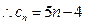
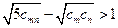 ,只要证:
,只要证: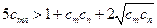
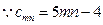 ,
,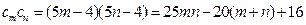
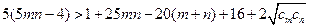 ,
, :
: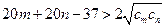 , 又
, 又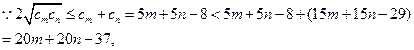
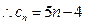
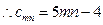 又
又
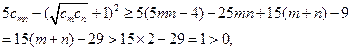
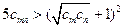 ,故
,故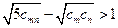


 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:高中数学 来源:不详 题型:解答题
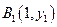 、
、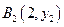 、…、
、…、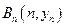 (n∈N)顺次为一次函数
(n∈N)顺次为一次函数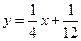 图像上的点,点列
图像上的点,点列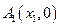 、
、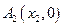 、…、
、…、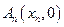 (n∈N)顺次为x轴正半轴上的点,其中
(n∈N)顺次为x轴正半轴上的点,其中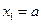 (0<a<1),对于任意n∈N,点
(0<a<1),对于任意n∈N,点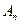 、
、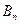 、
、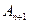 构成一个顶角的顶点为
构成一个顶角的顶点为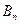 的等腰三角形。
的等腰三角形。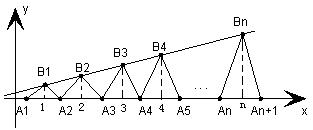
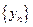 的通项公式,并证明
的通项公式,并证明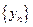 是等差数列;
是等差数列;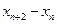 为常数,并求出数列
为常数,并求出数列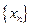 的通项公式;
的通项公式;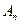
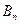
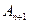 中,是否存在直角三角形?若有,求出此时a值;若不存在,请说明理由。
中,是否存在直角三角形?若有,求出此时a值;若不存在,请说明理由。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com