
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 ①写出命题P:“?x∈R,x2-2≥0”的否定形式为¬P即可判断①的正误;
②利用双曲线的定义可判断②的正误;
③利用“充分必要条件的概念可判断③的正误;
④写出命题“若x2-3x-4=0,则x=4”的逆否命题,可判断④的正误.
解答 解:①命题P:“?x∈R,x2-2≥0”的否定形式为¬P:“?x∈R,x2-2<0”,故①正确;
②双曲线上任意一点到左右焦点的距离的差的绝对值等于双曲线的实轴长,故②错误
③“m>n”不能推出“${(\frac{2}{3})^m}>{(\frac{2}{3})^n}$,反之,也不成立,故“m>n”是“${(\frac{2}{3})^m}>{(\frac{2}{3})^n}$的既不充分也不必要条件,故③错误;
④命题“若x2-3x-4=0,则x=4”的逆否命题为“x≠4,则x2-3x-4≠0”,故④正确;
综上所述,正确的个数是2个,
故选:B.
点评 本题考查命题的真假判断与应用,考查四种命题间的关系、全称命题与特称命题间的关系、充分必要条件的概念,属于中档题.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:高中数学 来源: 题型:填空题
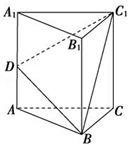 如图,已知球O的面上四点A、B、C、D,DA⊥平面ABC,AB⊥BC,DA=AB=BC=$\sqrt{3}$,则球O的体积等于$\frac{9π}{2}$.
如图,已知球O的面上四点A、B、C、D,DA⊥平面ABC,AB⊥BC,DA=AB=BC=$\sqrt{3}$,则球O的体积等于$\frac{9π}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
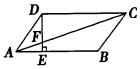
| A. | 54cm2 | B. | 24cm2 | C. | 18cm2 | D. | 12cm2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {$\frac{5π}{4}$} | B. | {$\frac{π}{4}$} | C. | {2kπ+$\frac{π}{4}$}(k∈Z) | D. | {kπ+$\frac{π}{4}$}(k∈Z) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 观察如图所示的正方形图案,每条边(包括两个端点)有n(n≥2,n∈N*)个圆点,第n个图案中圆点的总数是Sn.按此规律推断出Sn与n的关系式为( )
观察如图所示的正方形图案,每条边(包括两个端点)有n(n≥2,n∈N*)个圆点,第n个图案中圆点的总数是Sn.按此规律推断出Sn与n的关系式为( )| A. | Sn=2n | B. | Sn=4n | C. | Sn=2n | D. | Sn=4n-4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a,b中至少有一个为0 | B. | a,b中至少有一个不为0 | ||
| C. | a,b全为0 | D. | a,b中只有一个不为0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com